やさしいイラストを用いた解説で、難しい概念を体系的に学べるオンライン講座。機械や構造物、ロボット等に生じる力の計算がマスターできる！実践的な演習問題を通して力学的な挙動を解析する力が身につく。
円運動 ( 向心力、遠心力、慣性力 )について
半径r、速度vで等速円運動をする質点には、中心に向かい大きさが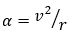
の加速度が生じます。
これが質点の円運動を可能にさせるもので、これを 向心力 (求心力ともいう) と言います。
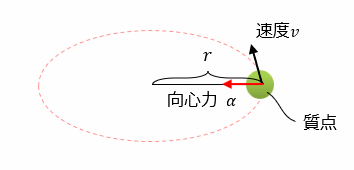
例えば、遊園地の回転ブランコの椅子に働く向心力は、ロープの張力の水平成分となります。
円運動する質点のつり合いを考えるときには、向心力(求心力)と逆向きで大きさが等しい力が働いていると仮定することにより可能となります。この仮定的な力を 遠心力 と言います。
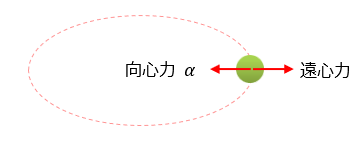
一般に、動的な質点のつり合いを考えるとき、それと方向が反対で、大きさの等しい力を仮定すると便利です。この力を 慣性力 といい、遠心力もその一つです。このように、動力学的問題を単に力のつり合いと言う静力学的問題に帰結する考え方を 「ダランベールの原理」 と言います。
いま、質量がmの物体に、力fが加わって、αの加速度を生じたとき、運動の方程式はニュートンの第2法則より f=mαとなります。 これに ―mα を考えれば、物体はつり合います。
α＝v2/ｒ でありますから、向心力 (求心力) の大きさは f ＝ mv2/ｒ という公式となります。
遠心力は向きが反対ですから、−mv2/ｒ となります。
糸に球をつけて円運動させている状態を考えたとき、糸が切れて向心力(求心力)が消滅すると、
球がその円運動の接線方向へ飛び去るのは、遠心力の働きではありません。向心力(求心力)が消えれば、遠心力もなくなります。球が接線方向に飛ぶのは、物体の慣性によります。
設計者に必要な６つの基礎知識（単位、数学、規格、力学、道具、形状）を学ぶ
工学知識きその基礎講座（Eラーニング）はこちらから
独自開発されたMONO塾の「ステップ式学習プログラム」＜法人採用実績：600社以上＞
カテゴリーメニュー
スポンサード リンク
