
機械や構造物、ロボット等に生じる力の計算がマスターできる!実践的な演習問題を通して力学的な挙動を解析する力が身につく。やさしいイラストを用いた解説で、難しい概念を体系的に学べる!
機械の動きについて(運動学)
ここまでで解説してきました内容は、「力のつりあいが取れている状態」、つまり「静力学」について解説してきました。
実際の機械は、停止状態のみではなく、さまざまな運動を行います。
そこでここからは、機械が時間とともに位置や速度が変化する運動学について解説いたします。
機械が行う運動には、
・直線運動
・円運動
・放物運動
・落下
などがあり、これら単体もしくは組み合わせにより、目的の運動を実現しています。
例えば、自動車のエンジンの場合、ガソリンの燃焼圧力により、ピストンが動き往復運動を行います。ピストンの往復運動は、クランクシャフトによって回転運動に変わります。
クランクシャフトの回転運動は、トランスミッション内に組みつけられた歯車などによって動力が伝達され、タイヤの回転運動に変わり自動車が動きます。
したがって、運動を伴う機械設計をおこなう場合は、これらのメカニズムを理解しておく必要があります。
直線運動
速度とは
時間の経過によって位置を変えることを「運動」といいます。
例えば直線運動の場合、移動した軌跡を結んだ線が直線になりますが、直線間の移動時間によって、私たちは「早い」とか「遅い」という表現をします。
これを定量的に表したものが速度です。
速度は一定時間(例えば1秒間)にどれだけ移動したかを表すものであり、
速度Vは
V = x/t [m/s]
で表します。
x : 移動した距離
t : 所要時間
速度の単位は、m/s 以外にも、m/min や自動車の速度計で使われる km/h などがあります。例えば15m/sの場合、1秒間に15m進みます。
なお、速度は方向を持っているため、ベクトル量となります。
加速度とは
停止している電車が走り出すとき、速度がしだいに増加します。走行中に自動車のアクセルを踏むと速度がしだいに増加します。
このように停止している 又は 移動している物体の速度がしだいに 増加 または 減少 する割合を加速度といい、次の式で表せます。
速度変化の割合 = (最後の速度v2−最初の速度v1)/所要時間
a = (v2-v1)/t
計算結果がプラスのときは、速度が増加し、マイナスのときは、速度が減少します。
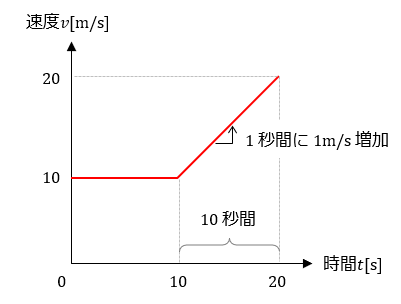
例えば、10 m/sで移動している物体が、10秒間に20 m/sの速度になった場合の加速度は、
加速度a = ( 20 - 10 ) /10 = 1 m/s2
となり、値がプラスなので、1秒間に1m/sずつ速度が速くなることを示しています。
円運動
円運動とは、ある一点を中心に一定の距離を保って回転運動することをいいます。
角速度とは
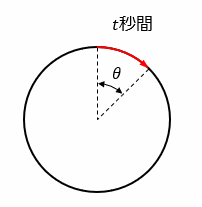
図のようにt 秒間に角度 θ だけ回転したとき、単位時間あたりの角度の変化を角速度といいます。
角速度 = 回転角度/所要時間
ω = θ/t
なぜ、直線運動のように、移動した距離を所要時間で割らないのかというと、同じ速度で回転していても回転半径によって速度が変わってしまうからです。
図のように一緒に回転している2つの円の回転速度は同じです。しかし、同じ時間に進むっ起動距離は異なってしまいます。

角速度を求める際に使われる角度の単位は、通常ラジアンが用いられます。
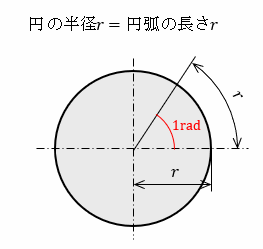
ラジアンとは、円の半径と円弧の長さが同じとなるような角度のことであり、図に示す角度を1rad(ラジアン)と呼びます。
 1 rad ≒ 57.3°
1 rad ≒ 57.3°
| 度 | ラジアン (rad) |
|---|---|
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 180° | π |
| 360° | 2π |
※ 1 rad を約3.14倍すると 180° である。π rad = 180°
角加速度とは
回転する物体の速度が増加または減少する割合のことを角加速度といい次の式で表します。
角加速度 = (最後の角速度ω2−最初の角速度ω」1)/所要時間
a = (ω2-ω1)/t [rad/s2]
回転速度
自動車のエンジンの回転単位にはrpmが使われています。
これは1分間にエンジンが何回転するかを表しています。
スポーツカーにはタコメーターが付いています。
下の写真のように、×1000 r/minと単位が表記されていますが、これはrpmと同じ意味です。
例えばメーターの針が3を指している場合は、3000rpmということです。
つまり、1分間に3000回転エンジンが回ります。

これを回転速度といいます。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



