やさしいイラストを用いた解説で、難しい概念を体系的に学べるオンライン講座。機械や構造物、ロボット等に生じる力の計算がマスターできる！実践的な演習問題を通して力学的な挙動を解析する力が身につく。
衝突と反発係数について
衝突と言う状態を知る前に理解しておかなければならないことがあります。
同じ物体であっても、それが静止しているか、運動しているかによって、その性質は大きく異なります。運動している物体は、衝突したとき他の物体に力を加えたり、仕事したりします。
しかしながらその物体が静止すれば、これらの働きは生じません。したがって、物体は運動していることによって、ある働きをする能力をもっていることになります。
このように物体自身の変化ではなく、状態の相違によってもつ性質を 物理的性質 と言いますが、特に運動状態でもつ性質には、「運動量」 と 「運動エネルギー」 があって、どちらも運動する物体のもつ重要な性質となってきます。
物体の運動量
物体が他の物体の力を作用したり、他の物体から力を作用されたりすれば、その力の向きによって、加速されたり減速されたりして速さが変化します。 このとき力の働きに比例して変化する物体のもつ物理量としては、物体の質量m と その速度υ の積mυ が変化するので、このmυを 運動量 と言います。
静止している物体に力Fを加えたときは、ニュートンの第2法則 (運動の法則) F=ma より加速度aは力に比例し、a＝F/mとなります。t秒後の速度υは、υ＝atとなり、このときの運動量mυは、mυ＝mat＝Ft で示されます。
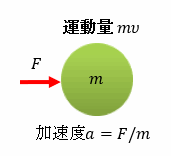
つまり、加えた力Fに比例した、運動量mυをもつことになります。
また、運動量の向きはその速度の向きによって異なりますので、運動量は大きさと向きをもつ量ですから、ベクトル量となります。 特に、Ftを力積 と言います。
運動量保存の法則
二つの物体A,Bが、たがいに作用、反作用の等しい大きさの力だけを受けている時は、一方の運動量の増加と他方の運動量の減少は等しく、A,Bの運動量の和は、力の作用した前後で変わりません。m1υ1＝m2υ2 で表され、これを 運動量保存の法則 と言います。
例えば、下図に示すように質量m1、m2の二つの物体A、Bが一直線上を運動しながら互いにゴムひもを通じてFの力を作用しあっているとき、ある瞬間の物体の速度を、右向きを正として、それぞれ、υ1、υ2とします。
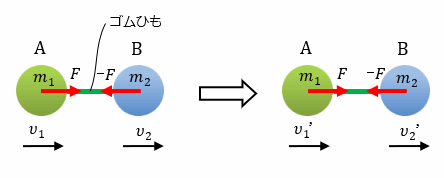
この状態から、何らかの変化があって、速度が、υ1‘、υ2’になったとします。この状態を運動量保存の法則で表しますと、m1υ1‘+ m2υ2’＝m1υ1+m2υ2となります。
衝突と反発係数
下図に示すようにAの速度υ1がＢの速度υ2より大きい（υ1＞υ2）とき、衝突 という状態が発生します。
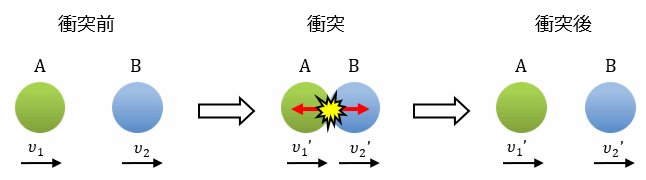
また、衝突前後の速度の比は「反発係数」といい、球の硬さなどによって決まる定数となります。
反発係数eは以下の式であらわされます。
e = 衝突後の速度／衝突前の速度 ＝ (υ1‘-υ2’) ／(υ1-υ2)
設計者に必要な６つの基礎知識（単位、数学、規格、力学、道具、形状）を学ぶ
工学知識きその基礎講座（Eラーニング）はこちらから
独自開発されたMONO塾の「ステップ式学習プログラム」＜法人採用実績：600社以上＞
カテゴリーメニュー
スポンサード リンク
