
機械や構造物、ロボット等に生じる力の計算がマスターできる!実践的な演習問題を通して力学的な挙動を解析する力が身につく。やさしいイラストを用いた解説で、難しい概念を体系的に学べる!
トラス構造とラーメン構造
トラス構造
トラス構造とは、複数の三角形による骨組構造のことであり、結合部である「節点」はボルトやピンなどで結合されています。
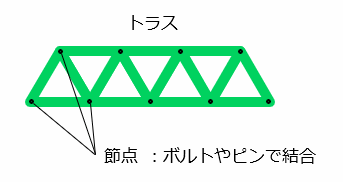
トラスの節点は自由度がないため動きませんが、相互に運動できるように結合されているため、部材を曲げようとする力である「曲げモーメント」が隣り合う部材で発生しません。そのため、荷重を加えたときに、部材には引張りまたは圧縮の力だけ働くことになります。
例えば、二等辺三角形の頂点に荷重を加えると、斜めの部材には「圧縮」の力、底辺の部材には「引っ張り」の力が加わります。
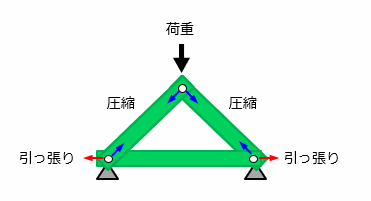
これは、結合部である節点が自由に回転できるからです。
このようなトラスの利点を活かして、橋、タワーなどの建築物、自転車やバイクのフレームなどがトラス構造になっています。
トラスを構成する三角形がひとつの同一平面内にあるものを、「平面トラス」、立体になっているものを「立体トラス」という。
<補足>
部材の節点に自由度をもたせ、回転させることができる機構は、「リンク機構」と呼ばれ、さまざまな機械の運動を実現させるためのものとなっている。
ラーメン構造
先ほどのトラスは結合部である節点がボルト等で結合されており、自由に回転できましたが、結合部が一体となっている構造を「ラーメン」と呼びます。
ラーメンの結合部は、互いに回転できないため大きな力が加わります。
そして、部材には引っ張り力や圧縮力などの軸力も多少加わりますが、部材を曲げようとする力(曲げモーメント)が発生します。この曲げモーメントの発生によって部材の強度を保つことができます。
ラーメン構造は複数の四角形の組み合わせにより構成されます。四角形であるため、力が加わると平行四辺形のように変形することになります。
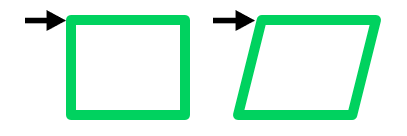
この変形を防ぐために結合部を強く接合します。

ラーメン構造は自由で大きな開口をとることが出来るため、鉄筋コンクリートなどの建築物に利用されています。
トラスの計算方法
図のような二等辺三角形のA点に荷重 10N が加えられたときの、各部材に発生する力を求めます。

A点に 10N の荷重が働くとき、このトラス構造は二等辺三角形であるため、B点、C点に働く 反力 RB , RC はそれぞれ 5N となります。
トラスの各節点はつりあっているため、各節点の水平分力と垂直分力の和はそれぞれゼロとなります。
・水平分力のつりあい
FBC + FABcos30 = 0 ・・・(1)
・垂直分力のつりあい
FABsin30 + RB = 0 ・・・(2)
(2)より、
FAB = - 5/sin30
= - 10N (圧縮力)
FAB = -10を(1)に代入
FBC= - FABcos30
= - (-10)×√3 /2
= 8.6N (引張力)
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



