未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
材料の曲げに対する強さ
部品にかかる外力はさまざまですが、その外力に対して如何に応力を低減できる設計を行えるのかが、設計者のスキルのひとつです。
ここでは、曲げる力に対しての応力低減について解説します。
曲げの力を受ける機械部品の代表的なものとして、軸があります。軸は軸受けにより支持されて、外力により曲げの力を受けることになります。
例えば、列車の車軸です。車軸は軸受けにより車両の荷重を受けています。車軸には曲げの力がかかります。
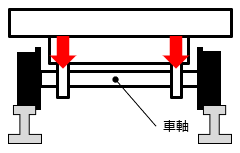
ここで、曲げの力が加わる軸を「はり」に置き換えて、どのような応力が働いているのか考えてみます。( ※ はりとは家屋の水平方向に使われる材料等の名称です)
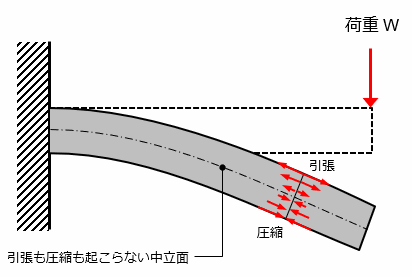
上図のように、「はり」に曲げの力が加わると、部材の上面は引っ張られ、部材の下面は圧縮されます。部材の中心部は、引張も圧縮も受けない中立面です。この場合、部材の上面で引張応力が最大となり、部材の下面で圧縮応力が最大となります。
以上のように、断面には 引張応力 と 圧縮応力 の2つの応力が発生していることになり、これらを総称して曲げ応力といいます。
部材に発生する曲げ応力は、部材の断面形状によって異なります。例えば、次に示す2つの部材では、B の方が曲がりやすいことは感覚的に理解できると思います。
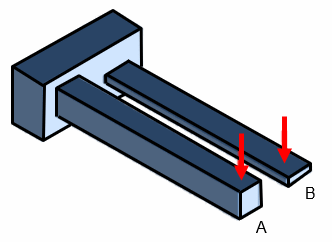
また、同じ断面形状であっても、曲げる方向によって曲がりやすさが異なります。
下図のAとBの断面形状および断面積は全く同じですが、Aの方が曲がりにくいということは感覚的に理解できると思います。
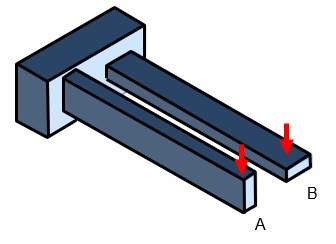
この曲がりやすさ、曲がりにくさ(剛性) を決めているのが 「断面係数」 です。
曲がりにくさを設計では「剛性」という言葉を使います。
※1 剛性(ごうせい)とは、曲げやねじりの力に対する変形のしづらさのことです。
・ 変形しにくい → 剛性が高い
・ 変形しやすい → 剛性が低い
剛性は設計者の共通言語なので覚えましょう!
曲げ応力(最大値)σmaxは、断面係数 Z と 曲げモーメント M により求めることができます。
σmax=M / Z
M:曲げモーメント
Z:断面係数
「曲げモーメントM」は、以下の場合、W × L で求められます。
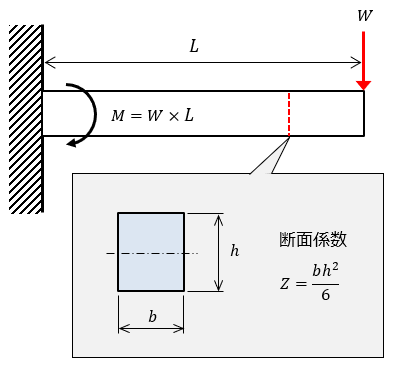
断面係数Zは断面の形状のみで決まる値です。
例えば、長方形の断面係数Zを求める公式は Z = bh2 / 6 です。
断面係数の公式は、必要に応じて「機械設計製図便覧」などで調べることができるので覚える必要はありません。以下に主な断面の断面係数を記載します。
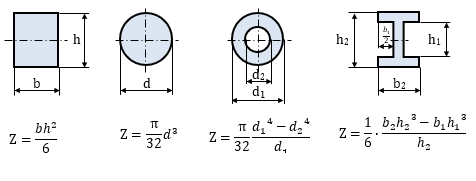
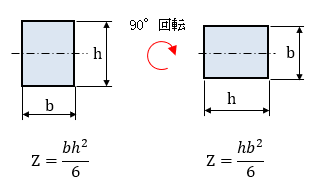
このように汎用的に使われる形状には断面係数Zが決まっています。ここで注意が必要なのは長方形のような場合です。長方形のように向きによって、中心軸からの高さが異なる場合は、断面係数Zの計算式が異なってきます。
H型鋼は材料を少なくすることができ、強度の高い構造であるため古くから建築部材として利用されている形状です。
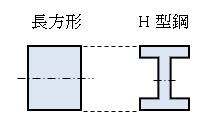
長方形のものと比較して、曲がりにくさも大きく変わらず、軽量化できるといったメリットがあります。
設計者は、このような知識を活用して、できるだけ少ない材料費で剛性の高い設計を行う視点を持つことが重要です。
また、コンピューターを使った強度解析においても、得られた結果に対して対策を講じる際に、これらの知識が非常に有効となってきます。
以上、曲げについての基本的な知識を解説してきました。
部材が破壊されるとき、多くのケースでこの曲げの力が加わることがあります。身近な例として、鉛筆を曲げることを考えてみましょう。鉛筆を引っ張ったりねじったりして壊すことは難しいですが、曲げると簡単に折れてしまいます。このように、曲げに対する理解は、日常生活においても重要です。
Eラーニングでは、材料力学の理論を感覚的に理解できるように工夫しています。初学者にも分かりやすいコースを提供し、実践的な知識を身につけることができます。ぜひ、弊社のEラーニングコースをご利用ください。

未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



