未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
ひずみとは
物体を引っ張ると、引っ張った方向に伸びます。この伸びた量を、変形量 といいます。
そして、元の長さに対する変形量の割合を「ひずみ」といいます。
従って、ひずみとは、物が伸びたときの比率のことです。下図の丸棒で具体的に説明します。
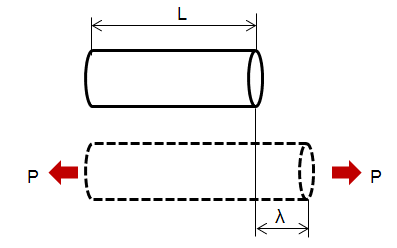
丸棒の元の長さを L とします。
そして、丸棒を引っ張ったときに伸びた量を、λ (ラムダ) とします。
ひずみは、元の長さに対する変形量ですので、次の式で表すことができます。
ひずみ ε = λ/L (変形量/元の長さ)
(ひずみはεという記号を使い、ε イプシロンと読みます。)
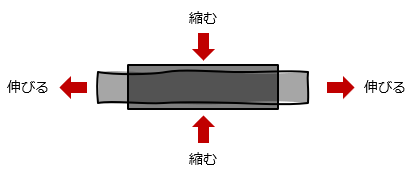
引張り方向のひずみを 「縦ひずみ」 といいます。
引張り方向に垂直なひずみを、「横ひずみ」といいます。
引張り方向に垂直な方向では、棒は縮みます。
この縮み量 δ(デルタ)を元の径で割った値が「横ひずみ」です。
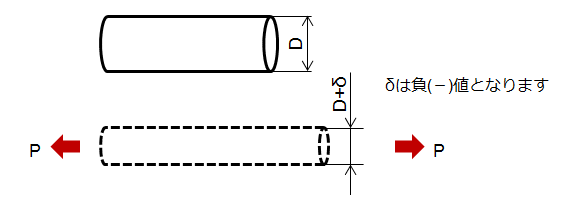
横ひずみは、縦ひずみと同様に次の式で計算されます。
ひずみ ε = δ/D (変形量/元々の直径)
D:棒の元の直径
δ:変形量
ポアソン比
物体がある方向に伸びると、その方向に垂直な方向は縮みます。例えば、下図のようなゴム製の板を引っ張ると、それに垂直な方向は縮みます。
この関係がポアソン比です。ポアソン比は、先ほど説明した 「縦ひずみ」 と 「横ひずみ」 から求めることができ、次の式で計算します。
ν = 横ひずみ/縦ひずみ
となります。
(ポアソン比は ν という記号を使い、ニューと読みます。)
材料によって、伸び方が当然異なりますので、材料別にポアソン比も異なります。
ポアソン比は材料によって異なります。以下に主な材料のポアソン比を示します。
- 鋳鉄 0.27
- 銅 0.343
- アルミニウム 0.345
- ゴム 0.46から0.49
伸びやすい材料ほど、ポアソン比の値が大きくなります。
圧縮ひずみ
圧縮ひずみは引張りのときのひずみと同様の考え方で求めることができます。
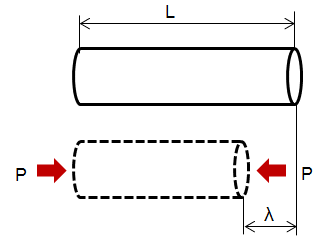
引っ張りと逆の方向に荷重がかかります。
縮んだ量をλとすると、ひずみεは、
ひずみ ε = λ/L (変形量/元々の長さ)
となります。
せん断ひずみ
物体を下図のように押した状態で、その一部を切り出すとひし形に変形していることがわかります。
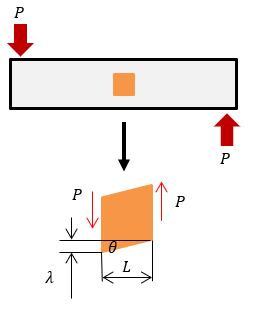
せん断を受けている微小距離をL、変形量λ、角度のずれθが生じたとき、
せん断ひずみγは、
γ = λ/L
(せん断ひずみは γ という記号を使い、ガンマーと読みます。)
また λ/l=tanθ であり、θは微小角度ですのでtanθ≒θとなり、せん断ひずみは変形角度と等しくなります。
以上、ここでは「ひずみ」について解説してきました。
ひずみは、物体が力によって変形する程度を表す指標です。このひずみを測定することで、物体に加わる応力を求めることができます。つまり、応力とひずみは密接に関連しており、どちらか一方を知ることで、もう一方を求めることができます。次のページで、これについて詳しく解説していきます。

未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



