未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
様々な応力
前のページでは「引張応力」について解説しました。次に、 「圧縮応力」、「せん断応力」、2種類の応力について解説します。
圧縮応力
圧縮応力は、引張応力と同様に理解しやすい応力です。圧縮応力とは、引張と反対方向に力が加わったときに発生する応力のことです。
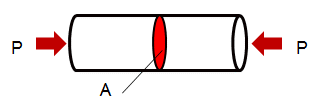
図のように圧縮方向に力を受けたときに、圧縮に抵抗する力が発生します。
その抵抗する力を断面積で割った値が圧縮応力となります。
計算式は引張応力と同様です。
圧縮応力 σ=P/A [N/mm2]
P [N] は、圧縮力です。
A [mm2] は、断面積です。
加えた力[N]を断面積[mm2]で割るので、圧縮応力の単位は N/mm2 となります。
せん断応力
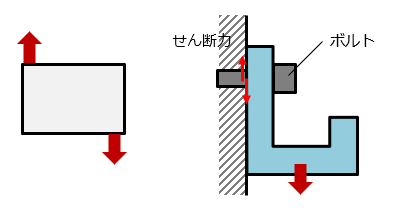
せん断応力は、引張や圧縮の応力と比較すると、少し感覚的に理解することが難しくなるかもしれません。例えば、せん断応力は、図のように、フックに与えた荷重によって、ボルトの断面を切断するように生じるような応力のことです。
引張応力や圧縮応力と同じ応力ですが、引張応力と圧縮応力が断面に対して垂直に生じる応力であるのに対して、せん断応力は、断面に平行に生じる応力となります。
応力値は下記の公式で求めることができます。
せん断応力 τ = P/A [N/mm2]
τ [N/mm2] は、せん断応力です。・・・「たう」と読みます。
P [N] は、荷重です。
A [mm2] は、ボルトの断面積です。
せん断応力は、断面に平行な応力ですので、物体がずれるときに発生します。ここで示したボルトのせん断の例は、せん断応力を理解するのにわかりやすい例です。
せん断応力が生じているということが、わかり難い例として、物体に引張、圧縮、曲げの力を加えた際に生じる、せん断応力があります。
例えば、地震で地面が引っ張られた場合です。 地面が斜めに割れる場合があります。
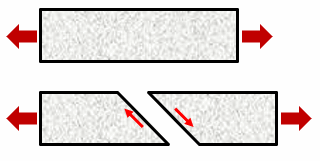
本を曲げると、それぞれにページが中でズレようとします。
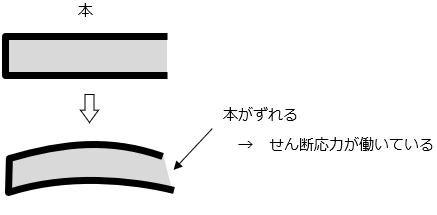
せん断に対して、抵抗する力が発生するからです。
このズレようとする力に抵抗する力が「せん断応力」です。
曲げ応力とせん断応力
曲げ応力とねじり応力の公式は少し複雑になるため、この章での解説を割愛することとし、後のページで詳しく解説します。まずは、このページで解説した引張、圧縮、せん断の3つの応力について確実に理解して次に進みましょう。
主応力
次に、主応力について説明します。はじめての方には少し難しい内容ですので、なんとなくの理解で大丈夫です。
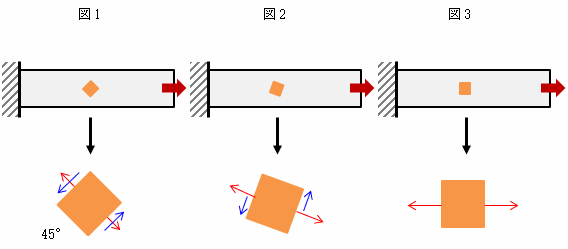
下図のように、梁に引張方向に力を加えた状態で、その物体を部分的に切り出した形状(図1)における応力を確認します。図に示す面には垂直応力(赤)とせん断応力(青)が生じています。
次に部分的に切り出した形状を少し傾けます。(図2)
すると、せん断応力は少し小さくなり、垂直応力が少し大きくなります。
次に、部分的に切り出した形状を引張方向と同じ方向に傾けます。(図3)。
すると、せん断応力は完全になくなり、垂直応力のみになります。
この応力を「主応力」といいます。つまり、せん断応力は、切り出した面によって、発生したりしなかったりするということです。
物体に様々な方向から荷重が加わった場合においても、主応力を求めることで、引張や圧縮の応力で評価することができるようになります。また、CAE解析(シミュレーション)においても、物体内部に発生する主応力で物が壊れるかどうかの評価を行う場合もあります。
以上、主応力について説明してきましたが、「主応力」という概念は初心者には難しかったかもしれません。従いまして、現時点では理解できなくても心配ありません。
しかしながら、設計に材料力学を取り入れて強度を確認するためには、この概念を理解することが不可欠です。学習を進めて知識がついてきた段階で、改めて主応力について理解を深めるように心がけましょう。
なお、弊社のEラーニングでは初心者でもわかりやすいように、ビジュアル的に説明したコンテンツをご用意しています。主応力をはじめとする材料力学の難しい概念も、わかりやすく理解できるように工夫しています。ぜひ、設計者に必要な知識を身につけるためのEラーニングをご活用ください。

未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



