未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
応力とひずみ
ここまでに応力とひずみについて解説してきました。この応力とひずみは比例の関係にあります。例えば、棒を引っ張っていくと ひずみ が大きくなりますが、それに応じて応力も大きくなります。
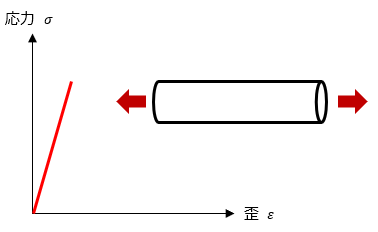
但し、応力とひずみが比例するのは、ひずみが小さな時のみです。ひずみが大きくなると、後程解説しますが、比例関係を保てなくなります。
(※材料によっては比例にならないものもある)
応力とひずみの線図は、「引張試験機」 で測定して作成することができます。材料をJISで決められたサイズにカットし、試験機にセットした後に上下方向に引っ張って測定します。
引張試験機で試験片に荷重を加えていくと、下図のように応力とひずみが比例します。また、比例区間を超えて下図の位置までひずみが増えた区間を 「弾性域」 といいます。
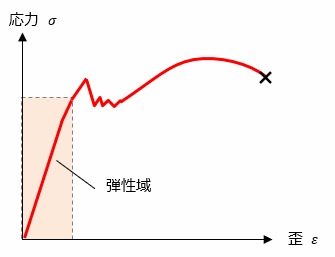
そして、弾性域におけるグラフの傾きを「ヤング率(弾性率)」といい、E で表します。ヤング率は変形のしにくさを表す物性値であり、材料によって異なります。また、このように応力とひずみの比が等しくなる法則を「フックの法則」といいます。フックの法則は以下の式で表されます。
σ:応力 [N/mm2]
E:弾性率 [N/mm2]
ε:ひずみ
中学生の時に学んだ、2点を通る直線の方程式である y = ax と同じ考え方ですね。
降伏点
応力とひずみの関係は、ある一定の応力に達すると、比例しなくなります。そして、弾性域を超えた先にある限界点を、「降伏点」 と呼びます。
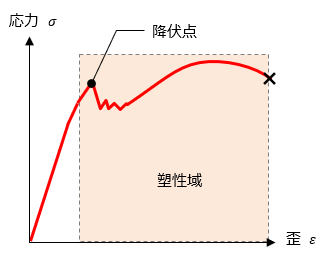
弾性域では、材料に加えた力を解除すると形状は元に戻ることができます。しかし、降伏点を超えると元に戻ることができません。弾性域を超えた領域を、「塑性域」 といいます。塑性域を超えて、ひずみを増やしていくと材料は破断します。
以上、応力とひずみの関係について解説してきました。特に応力について理解することは、材料の強度や耐久性を計算する上で非常に重要です。応力の値を正確に求めることで、材料がどのような状態で力に耐えられるかを評価することができます。これにより、材料の強度計算や設計の最適化が可能になります。ぜひ、応力やひずみについてしっかり理解して、より高度な設計を目指しましょう。
なお、ここでは文章のみで解説してきましたので、少し伝わりにくい部分もあったと思いますが、弊社のEラーニングではビジュアル的に学べる工夫がされており、初心者にわかりやすく作っています。
例えば、応力とひずみの関係についての説明があるシーンでは、実際に材料に力を加えることで変形が生じるアニメーションや、異なる材料に力を加えたときの応力とひずみの違いを比較するグラフなど、視覚的な要素を取り入れています。
また、視覚的な工夫だけでなく、実際の設計に役立つ具体的な例や演習問題も用意しています。これにより、受講者は理論だけでなく実践的な知識も学ぶことができます。
さらに、分からない箇所があった場合には、教材を作成した専門家が受講者の疑問や質問に対応するサポートも提供しています。このように、Eラーニングでは視覚的な要素や実践的な演習、サポート体制など、従来の教材にはなかった多彩な工夫が施されています。

未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



