未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
応力とは
材料力学を学ぶ上で、まずはじめに理解しなければならないのが応力です。
設計においても、応力は頻繁に使われます。
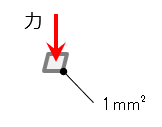
応力とは、部材内に発生している単位面積あたりの力です。具体的に言うと、1mm2あたりにかかる力が応力です。大根が1kgあたり100円と表現しているのと同じ感覚です。
部材内に発生する応力が大きくなると部材は破壊します。大根も1kgあたりの値段が高騰すれば家計が破たんするかもしれません。具体的に説明していきますね。
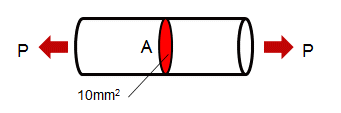
例えば、断面積が10mm2 棒を1000N の力で引っ張った時に発生する応力は、引っ張る力 (P) を棒の断面積 (A) で割った値となります。
応力σ = 引っ張る力 P / 断面積 A
= 1000N / 10 mm2
= 100 N/ mm2
※応力は σ (シグマ) という記号を使います。
少し説明が難しくなりますが、もう少し具体的に説明します。厳密には下記を理解する必要がありますが、読み飛ばして頂いても、この後の解説は理解できるので大丈夫です。
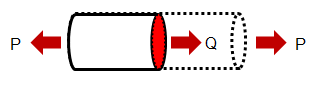
先ほどの図の仮想の断面Aの位置で切断した図で考えてみます。
断面Aには、変形に対して抵抗する内力Qが働きます。
内力は P に応じて生じる作用反作用の力です。
例えば、手を引っ張られた時に、それに抵抗する力が内力です。
引っ張られる力と同じ力で引っ張り返せば釣り合いが取れます。
この内力Qの単位面積あたりの力が応力となります。
従って応力σは Q / A (力Qを断面積Aで割った値)となります。
内力QとPは釣り合っていますので、Q=Pとなります。
応力 σ = Q / A = P / A
P は力です。
A は断面積です。
力を断面積で割るので、応力の単位は N/mm2 となります。
次に、断面が途中で細くなっている部材で同様の力をかけてみます。この場合、どの部分から壊れるか一目瞭然ですね。部材はもっとも弱いところから壊れます。
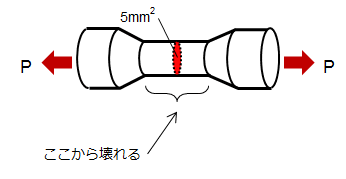
壊れる部分の応力を求めてみます。断面積は先ほどの10 mm2の半分の5 mm2したとき、
σ= 1000N / 5 mm2 = 200 N/ mm2
断面積が半分になり、応力が2倍になったことがわかります。このように応力は部材の材料に関係なく、形状によってきまるものであることが理解できます。つまり、形状を変えることによって、応力が高くなったり、低くなったりするということです。
設計する際には、機械や製品が壊れないように高すぎる応力が発生している箇所は、形を大きくするなどして、応力を下げる必要があります。逆に、応力に余裕のある場合は、形を削って軽量化させる必要があります。
以上、ここまでに説明した部材では、部材を引っ張ったときの応力は、どの断面を切っても同じ応力値となるため、とても分かりやすい例です。
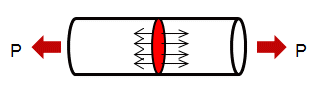
しかし、実際の機械や製品に生じる応力は様々な方向、様々な大きさで働く場合もあります。さらに、曲げたり、ねじったり、など複合的な力が加わる場合もあり、応力を簡単に求めることができないケースも出てきます。
次に、引張応力以外の様々な応力について解説します。

未経験でも安心!職場や自宅で学べる材料力学オンライン講座。掛け算や割り算ができる方なら大丈夫!充実の演習を通して、強度や剛性といた強度計算ができるように徹底的に学べます。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



