動画で学ぶシリーズ >>｜単位と力学｜設計きそ｜図面｜材料力学｜材料（金属・樹脂..）｜
熱応力
「熱膨張」 という言葉を聞いたことがあると思います。
多くの方は、小学校理科で空気を温める実験で熱膨張を経験していると思います。熱により材料の体積が膨張する（大きくなる）ことです。材料は温度によって、伸びたり縮んだりします。従って、温度変化が大きな環境で使用する機械や製品の場合、熱膨張を考慮した設計が必要です。
熱膨張を考慮した代表的な設計の事例として、鉄道のレールがあります。レールは一本物ではなく、短い複数のレールを繋ぎあわせて作ります。レールを短くしているのは「製造することができない」 「運搬が困難である」 等の理由以外に、熱膨張の影響を避ける目的があります。
レールは夏場には高温となり伸びます。逆に冬場は縮みます。そのため「遊間」という継ぎ目を作り、隙間を設けています。この隙間がそれぞれのレールが伸びた際にぶつからない役割を果たします。
もし、隙間がなければ夏場に膨張したレールがぶつかり合い、逃げ場を失ったレールが曲がったり、盛り上がったりします。これは重大な事故に繋がります。
従って、設計を行う場合、温度変化を考慮した設計が必要となってきます。
レールの場合は隙間が必要ですが、機能上必ずしも隙間を必要としている訳ではありません。隙間がない場合は、温度の変化により、その物体の内部に応力が発生します。
例えば、以下のように常温（T1）から高温（T2）になった場合、材料は伸びます。
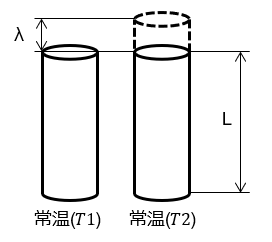
このときの伸び量をλとすると、
λ ＝ α×（T2 − T1）×L
α：線膨張係数 T１：上昇前温度 T2:上昇後温度
の公式で伸びた量を計算することができます。
線膨張係数は材質毎に決まっています。線膨張係数は、1mあたり1℃（1K）上昇するとα μm 伸びる係数のことです。
以下に主な材質の線膨張係数を示します。
表．線膨張係数α（×10-6／K）
| 材質 | 線膨張係数α |
|---|---|
アルミニウム |
23.1 |
金 |
14.2 |
銀 |
18.9 |
銅 |
16.5 |
タングステン |
4.5 |
チタン |
8.6 |
鋳鉄 |
11.7 |
炭素鋼 |
12.5 |
材料に伸びが発生しないように両端が固定されている場合、本来伸びるはずであった λ 分だけ縮めたことと同じとなります。縮めたため、内部にはひずみが発生します。このひずみを 熱ひずみ といいます。
熱ひずみεは
ε＝α（T2-T1）
の式で求められます。
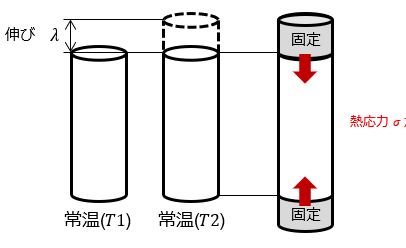
従って、材料内に発生する応力はフックの法則により
σ＝Eε＝Eα（T2-T１）
となります。
このときの応力を 熱応力 といいます。
（例）
長さ0.2m の両端固定した炭素鋼の棒が２０℃から８０℃に上昇したときの応力σは
σ＝Eε＝Eα（T2-T1）＝20.5×104×12.5×10-6×（80−20）＝153.75N/mm2
はじめての方へ