熱力学におけるエントロピー
熱力学第二法則で解説しましたが、エントロピーとは分子の乱雑さのことを表しています。これを熱力学の視点から解説していきます。水にインクを一滴垂らすと外側に広がっていきます。インクが広がった状態は分子が乱雑になっており、「エントロピーが大きい」です。
熱力学第二法則においてエントロピーは、熱は、熱いものから冷たいものへ移動するが、冷たいものから熱いものへは移動しないような「不可逆現象」においては増大し、「可逆現象」では一定となります。
エントロピーは次の式で表されます。
ΔS ：エントロピーの増加量
T：温度
ΔQ：加えた熱量
※ Δの読み方 → デルター
温度（T）に、微小の熱量（ΔQ） が加わったときのエントロピーの変化量（ΔS）は、
「加えられた熱量（ΔQ）」 を 「温度（T）」 で割った値となります。
(式1)は可逆現象でのみ成立します。
次にこの理由について、カルノーサイクルを用いて説明します。
カルノーサイクルとエントロピー
最も効率のよいエンジンとされるカルノーサイクルでエントロピーの変化について考えてみます。
（カルノーサイクルについての詳しい解説はこちらからどうぞ
→ カルノーサイクルとは ）
先ほど、カルノーサイクルについて、前述のページでは、P-V線図（圧力と体積の関係）を用いて紹介しましたが、熱の出入りを分かりやすくする目的で、T-S線図（温度とエントロピーの関係）で説明していきます。
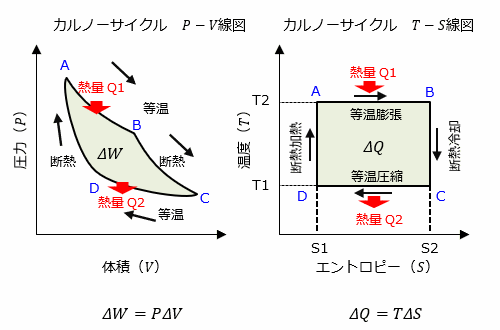
カルノーサイクルにおいて、外部へ行う仕事は、P-V線図の「線で囲われた面積」となります。
式で表すとΔW=PΔVとなります。（※ 仕事とエネルギー）
ここで、エントロピーの式 ΔS = ΔQ／T を変形すると、ΔQ=TΔS となり、ΔW=PΔV と似た式で表すことができます。
以上より、
上左図（P-V線図）で外に行った仕事は、薄緑色の面積 ΔW であることから、
上右図（T-S線図）で外から受け取った熱量は、薄緑色の面積 ΔQ となることが理解できます。
また、カルノーサイクルの解説ページで説明しましたが、
外に行った仕事 ΔW は ΔW = Q1-Q2 であるため、
ΔWとΔQ （= Q1-Q2）は等しく、上図の線で囲われた薄緑色の面積は等しいことがわかります。
カルノーサイクルは、逆が成り立つ可逆現象です。また、このときエントロピーは増大しません。従って、エントロピーの増加量 ΔS=0 となります。
等温変化において、シリンダーとピストンの間に摩擦熱が発生すると仮定すると、仕事に変換されない熱量が発生するため ΔS>0 となりエントロピーが増加します。
以上より、エントロピーが増加しないサイクルの場合は、熱が仕事へ、仕事が熱へ可逆変化することができ、熱効率が最大となります。一方、摩擦熱が発生するようなエントロピーが増加するサイクルの場合は、熱効率が下がることになります。
独自開発されたMONO塾の「ステップ式学習プログラム」＜法人採用実績：600社以上＞
カテゴリーメニュー
スポンサード リンク
