仕事とエネルギー
力が一定の場合の仕事の求め方
これまでの解説で、熱は仕事であり、エネルギーであることを理解して頂きました。
次にさらに詳しく理解して頂くために、仕事の求め方について説明します。高校物理では、仕事を求める式として下記を学びます。
Ｗ＝ＦＬ
Ｗ：仕事
Ｆ：力
Ｌ：移動距離
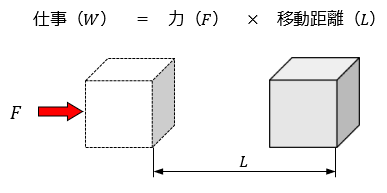
仕事は力×移動距離で求めることができます。この式は熱力学で非常に重要な式となります。
例えば、１０Ｎの力で１０ｍ荷物を移動させたときの仕事は
Ｗ＝１０Ｎ×１０ｍ＝１００Ｎ・ｍ のようにして求めることができます。
これをグラフで表すと、下図のようになります。
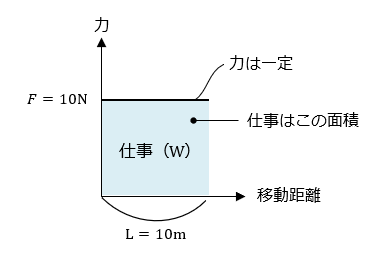
仕事は 力×移動距離なので、ちょうどグラフの面積を求めることが、仕事を求めることになります。但し、この公式は、加える力が一定のときのみ使うことができます。
力が変化する場合の仕事の求め方
次に物体がバネで固定されている状態で、移動するにつれて力が変化する場合の仕事を求めてみます。
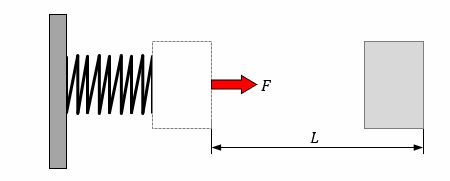
フックの法則からバネにかかる力Fは F = Kx で表されます。
力と移動距離の関係をグラフにすると図のようになります。初期段階ではバネを引く力は小さくてすみますが、バネが伸びるに従って大きな力を必要とします。
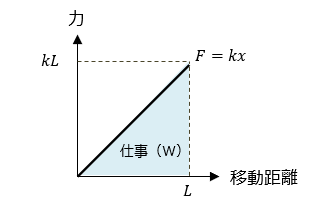
「力が一定」 のときと同様に仕事をグラフの面積から求めると、
仕事W ＝ グラフの面積 ＝ 三角形の面積
＝底辺×高さ÷２
＝L×KL÷２
Ｗ＝Ｌ×ＫＬ÷２＝1/2KL2
ピストンが動いたときの仕事の求め方
ここまでの内容を踏まえて熱力学の話に戻ります。次の図のようにシリンダーを熱で温めると、ピストンが圧力を受けて上昇します。これは熱がエネルギーに変わり仕事をしたからです。
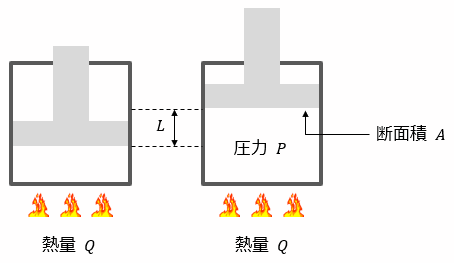
この場合の仕事（W）は、圧力が一定なため W = FL で求めることができます。
ピストンにかかる力は、 力（F）＝圧力（P）×断面積（A）で求めることができるため、ピストンがが動いたときの仕事は、 W = PAL となります。
※ 圧力とは単位面積あたりの力なので、力は圧力に断面積をかければ良い。
例えば、圧力P＝5N/mm2 が10mm2の断面積にかかる力Fは、
F = 5N/mm2×10mm2 = 50N
また、AL は 断面積×ピストンの移動距離 なので増えた体積（ΔＶ）です。
（Δはデルタと読み、変化量を示す記号のこと）
従って、
仕事（Ｗ）＝ＰＡＬ
＝ＰΔＶ と書き換えることができます。
これをグラフで表すと下図のようになります。
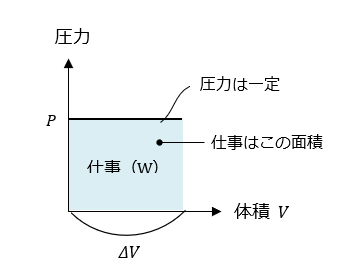
つまりピストンに加えた熱Qが仕事Wに変わったということです。しかし、『 加えた熱量Q 』 ＝ 『 ピストンがした仕事W 』 にはなりません。 実際は Q＝ΔU＋Wとなります。これを熱力学の第一法則といいます。次にこのことについて解説します。
独自開発されたMONO塾の「ステップ式学習プログラム」＜法人採用実績：600社以上＞
カテゴリーメニュー
スポンサード リンク
