熱力学第一法則

熱力学第一法則は次の式で表されます。

Q = ΔU + W

Q は加えた熱量
ΔU は内部エネルギーの増加量
W は行った仕事です。

式だけ見ても良くわかりませんので具体的な例で説明します。

下図のように ピストンを固定した状態 で、シリンダーを熱量（Ｑ）で加熱します。

すると内部の気体の温度が上昇して、圧力が上昇します。

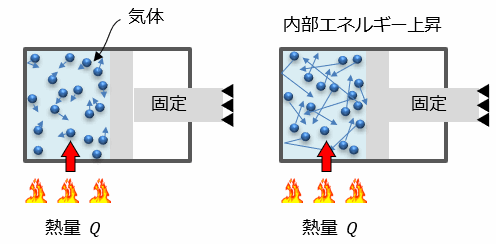
この場合、加えた熱量（Ｑ）は全て温度の上昇「＝内部エネルギーの上昇（気体の場合）」に変化します。

従って、これを式にすると、

Q = ΔU　となります。

次にピストンを固定せずに熱量（Ｑ）を加えてみます。

すると内部の分子の運動が激しくなることで温度が上昇して、空気が膨張しピストンが移動します。

つまり、内部の気体が 「外部に対して仕事を行った」 ということです。

ここで、ピストンは大気の圧力（P）とバランスを取りながら移動するため、内部圧力は常に一定となります。このときの仕事Ｗは圧力が一定であるため、 W = PΔV となります。（※詳しくは仕事とエネルギーで解説）

従って、加えた熱量（Ｑ）が内部エネルギーの上昇（ΔＵ）とピストンを動かすという仕事（Ｗ）に変換されたということになり、

Q = ΔU + W
　= ΔU + PΔV

が成り立ちます。

熱と仕事は同じものであり、「熱から仕事へ」、「仕事から熱へ」　変換することができ、その間においてはエネルギーが保存されます。

これを　熱力学第一法則　といいます。

内部エネルギーとは

ここで内部エネルギーについてもう少し理解を深めます。

内部エネルギーとは、物体内部に持っているエネルギーのことです。

物体内部のエネルギーとは、

１．分子の運動によるエネルギー
２．分子間で働く力によるエネルギー

です。

この２つのエネルギーを合わせて　内部エネルギー　といいます。

分子は熱を受けることで激しく運動を行います。

固体と液体は、分子間で働く位置エネルギーを持っています。
しかし、気体では分子間で働く位置エネルギーを無視することができます。

気体は、「分子間で働く位置エネルギー」を無視することができます。

前の項目で解説したピストンの例は、熱を受けたのは「気体」でしたので、「分子間で働く位置エネルギー」を無視することができます。従って、ピストンのケースでは、　内部エネルギー（ΔU）　＝　分子の熱運動による運動エネルギー　となります。

≪前のページへ　　次のページへ≫

＼機械設計者向け「eラーニング」でスキルアップ！／

独自開発されたMONO塾の「ステップ式学習プログラム」＜法人採用実績：600社以上＞