力学の公式一覧
力の合成
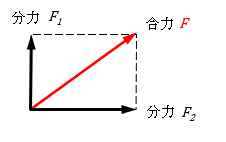
2つの力が直角の場合 |
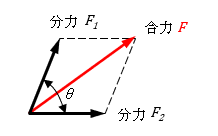
2つの力が\(\theta\)で交わる場合 |
|---|---|
|
\( F=\sqrt{ F_1^{2}+F_2^{2}} \) |
\( F=\sqrt{ F_1^{2}+F_2^{2}+2F_1F_2\cos\theta} \) |
力のモーメント
曲げモーメント\(M\) [N・m]は、力\(F\) [N]×腕の長さ\(l\) [m]で求めることができる。
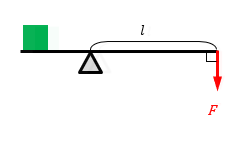
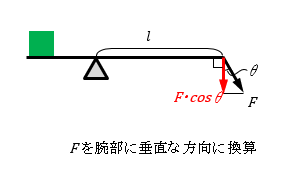
| 力が腕部に垂直な場合 | 力が腕部に対して傾いている場合 |
|---|---|
|
\( M=Fl \) |
\(M=Fcos\theta・l \) |
≪モーメントの単位≫
・SI単位 : N・m
・工学単位(重力単位) : kgf・m
・単位換算 : 1N・m = 0.10197 kgf・m
力の偶力モーメント
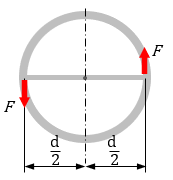 |
\( M=F(\frac{d}{2})+F(\frac{d}{2})=Fd \) |
運動方程式
物体に力\(F\)を与えると、物体に加速度\(a\)が生じる。
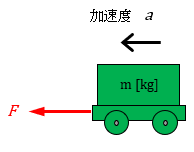 |
\( F=ma= \frac{W}{g}a \)
\(\quad F\) [N] :物体に作用する力 |
向心力と遠心力
 |
・向心力
・遠心力
\(\quad F\) [N] :向心力、遠心力 |
等速直線運動 (=等速度運動)
時間\(t\)秒[s]間に変位(距離)\(x\)[m]だけ移動したときの速度\(v\)[m/s]を求める公式。
 |
速度= 変位÷所要時間
\(\quad v= \frac{x}{t}\quad \) [m/s] |
等加速度直線運動 (=等加速度運動)
時間\(t\)秒[s]間に速度が\(v_0\)[m/s]から\(v\)[m/s]に変化したときの加速度\( a\)[m/s2]を求める公式。
 |
加速度= (終速度ー初速度)÷所要時間
\( \quad a = \frac{v-v_0}{t}\quad \) [m/s] |
上記式より下記t秒後の速度の式が得られる。
また、このとき物体が動いた距離を\(x\)[m]は、下記の公式で求めることができる。
 |
\(t\)秒後の速度:\( v=v_0+at \) |
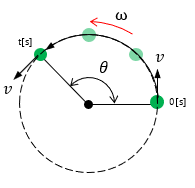
等速円運動
■角速度
時間\(t\)秒[s]間に角度\(\theta\)[rad]だけ回転したときの角速度\(\omega\)[rad/s]を求める公式。
 |
角速度= 回転角÷所要時間
\( \quad \omega= \frac{\theta}{t}\quad \) [rad/s] |
■周速度
回転半径\(r\)、\(t\)秒[s]間に角度\(\theta\)[rad]だけ回転したときの周速度\(v\)[m/s]を求める公式。
※周速度は半径の大きさで変わる。例えば半径が2倍になると周速度も2倍になる。
 |
周速度= 円弧の長さ÷所要時間 |
回転直径\(D\)[m]、回転数\(N\)[[rpm]で回転しているときの周速度\(v\)[m/s]を求める公式
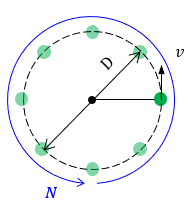 |
周速度=(\(\pi\) ×直径×回転数)÷60
\( v= \frac{\pi×D×N}{60}\quad \) [m/s] |
■回転速度
1分間あたりの回転数を回転速度\(N\)といい単位は[rpm]を使用する。角速度を\(\omega\)[rad/s]とすると、回転速度\( N \)[rpm]は次の式で表される。
※rpmはr/min(アールパーミニット)、又は、min-1とも表記される。
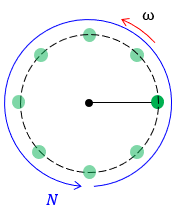 |
回転速度= (60×角速度)÷2 \(\pi\)
\( N= \frac{60 \omega}{2 \pi} \) |
≪回転速度(回転数)rpmを角速度[rad/s]への換算式≫
角速度= (2\(\pi\)×回転速度)÷60 \(\quad \omega= \frac{ 2\pi N}{60}\quad \) [rad/s]
等角加速度運動
時間\(t\)秒[s]間に角速度が\(\omega_0\)[rad/s]から\(\omega\)[rad/s]に変化したときの角加速度\( \dot \omega\)[rad/s2]を求める公式。
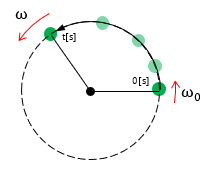 |
角速度=(最後の角速度ー最初の角速度)÷ 所要時間
\(\dot \omega=\frac{\omega-\omega_0}{t} \) |
上記式より下記t秒後の角速度の式が得られる。
また、このとき物体が回転した角度\(\theta\)[rad]は、下記の公式で求めることができる。
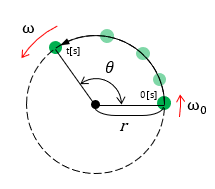 |
\(t\)秒後の角速度:\( \omega=\omega_0+\dot \omega t \) |
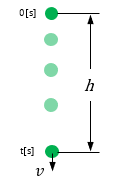
自由落下運動(下向き+)
\(t\)秒[s]経過したときの速度\(v\)[m/s]と距離\(h\)[m]を求める公式。但し、重力加速度は \(g\) [m/s2]とする。
 |
\(t\)秒後の速度:\(v=gt\) |
鉛直下向投射(下向き+)
初速度 \(v_0\),\(t\)秒[s]経過したときの速度\(v\)[m/s]と距離\(h\)[m] を求める公式。但し、重力加速度は \(g\) [m/s2]とする。
 |
\(t\)秒後の速度:\(v=v_0+gt\) |
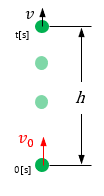
鉛直上向投射(上向き+)
初速度 \(v_0\),\(t\)秒[s]経過したときの速度\(v\)[m/s]と距離\(h\)[m] を求める公式。但し、重力加速度は \(g\) [m/s2]とする。
 |
\(t\)秒後の速度:\(v=v_0-gt\) |
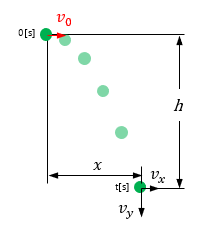
水平投射
初速度 \(v_0\),\(t\)秒[s]経過したときの速度\(v\)[m/s]と距離\(h\)[m] を求める公式。但し、重力加速度は \(g\) [m/s2]とする。
 |
水平方向 |
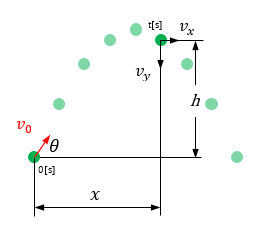
斜方投射
初速度 \(v_0\),\(t\)秒[s]経過したときの速度\(v\)[m/s]と距離\(h\)[m] を求める公式。但し、重力加速度は \(g\) [m/s2]とする。
 |
水平方向 |
機械の仕事と動力の公式
直線運動の仕事
物体を力\(F\) [N]で\(x\)[m]の距離を動かした時の仕事\(W\) [J]を求める公式
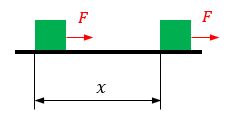 |
仕事=力×移動距離 \(W=F・x\) [J]又は[N・m] |
※1[J]=1[N・m]
直線運動の動力
物体を力\(F\) [N]で\(t\)秒[s]かけて\(x\)[m]の距離を動かした時の動力\(P\) [W]を求める公式
 |
動力= 仕事÷時間
動力=(力×移動距離)÷時間
動力=力×速度 |
※1[W]=1[J/s]
回転運動の仕事
物体をトルク\(T\) [N・m]で\(\theta\)[rad]回転させた時の仕事\(W\) [J]を求める公式
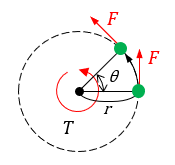 |
仕事=トルク×回転角
※トルク\(T = Fr\) |
回転運動の動力
物体をトルク\(T\) [N・m]で\(t\)秒[s]かけて\(\theta \)[rad]の回転させた時の動力\(P\) [W]を求める公式
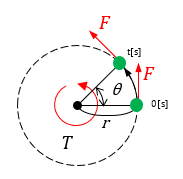 |
動力= 仕事÷時間
動力=(トルク×回転角)÷時間
動力=トルク×角速度 |
回転速度\(N\)[rpm]の場合の公式
\( 動力=トルク× \frac{2\pi×回転速度}{60}\hspace{2em} P= T・ \frac{2\pi N}{60}≒ \frac{T N}{9.549}\) [W]又は[J/s]
工学単位を使った動力の計算式 トルク \(T\) [kgf・m]
\( 動力= \frac{ 2\pi TN}{60×102} \) [kW] ≒ \( \frac{T N}{975} \) [kW]
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク