角度(勾配)計算ツール
設計形状に傾斜(勾配)をつけることが多々あります。
こちらの計算ツールを使うと、直角三角形の2辺から傾斜角度を簡単に求めることができます。
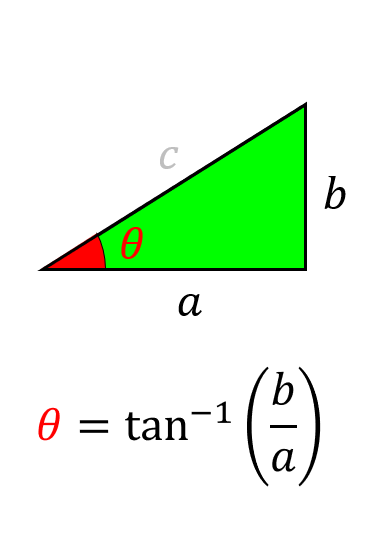
辺abが分かっている場合
| θ | = | - rad |
| = | - 度 | |
| = | - | |
| 辺c | = | - |
θ = TAN-1(b/a)×180/π =
度
c = √(a2 + b2) =
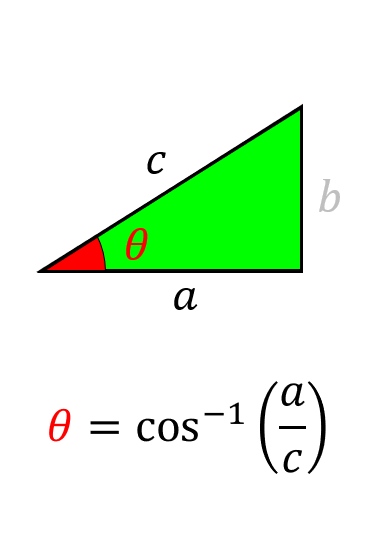
辺acが分かっている場合
| θ | = | - rad |
| = | - 度 | |
| = | - | |
| 辺b | = | - |
θ = COS-1(a/c)×180/π =
度
b = √(c2 - a2) =
辺bcが分かっている場合
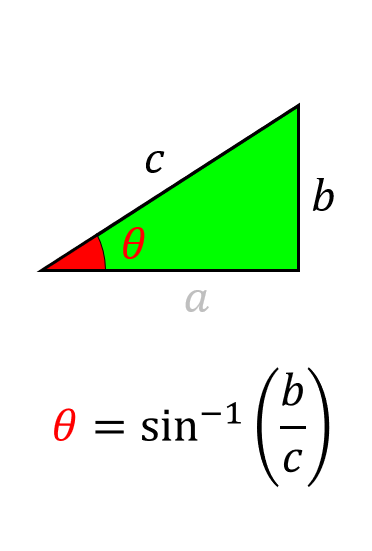
| θ | = | - rad |
| = | - 度 | |
| = | - | |
| 辺a | = | - |
θ = SIN-1(b/c)×180/π =
度
a = √(c2 - b2) =
斜面の角度の計算についての解説
斜面の角度は、直角三角形の2辺の長さが分かれば計算できます。例えば、aとbの長さが分かっている場合、三角関数 tanθ=b/a より θ=tan-1(b/a)で角度の計算ができます。
この式で求まる角度θは、弧度法のラジアンです。
角度の表し方には、弧度法と60分法があります。
弧度法の単位が「ラジアン」rad
60分法の単位が「度」°
です。
弧度法とは
弧度法は、1つの円において,「半径と等しい長さの弧に対する中心角の大きさ」を 1[rad](ラジアン) と定義し,1[rad] を単位とする角度の表し方です。
(1ラジアン=57.3度となります。)
60分法とは
円の1周を360度として角度を表す方法です。
60分法の方が慣れているのでわかりやすいですが、技術計算や数学では弧度法を使うケースがありますので単位換算できるようにしておく必要があります。
弧度法と60分法の関係
弧度法(ラジアン)と60分法(度)の関係は、
度=ラジアン × 180 ÷ 円周率 です。
1rad=57.3度
1度=π/180rad
角度(度・分・秒)についての解説
角度の単位は、「度」または「°」で表します。
1分は1度の「60分の1」の角度と定義されています。
例えば30分は、0.5度です。
記号は ' を使います。
1秒は1度の「3600分の1」の角度と定義されています。
記号は " を使います。
1度より小さな角度をCAD図などで示す場合は、「度分秒」が使われることがあります。'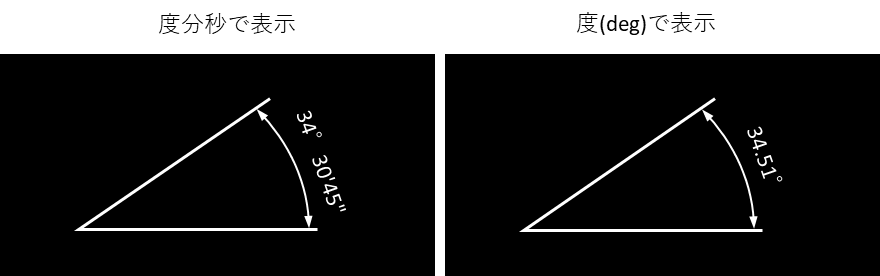
辺の長さの計算についての解説
直角三角形は、2辺の長さをa,bとし、斜面(勾配)の長さをcとすると「三平方の定理」より次の式が成立します。
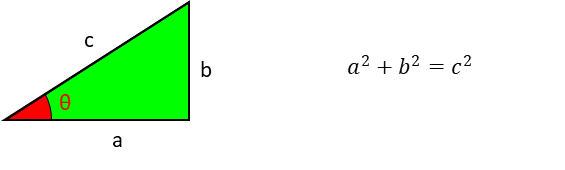
従って、3つある辺の内、2辺が分かれば残りの1辺の長さがわかります。
例えば、bとcが分かっていてaを求める場合の式は以下となります。
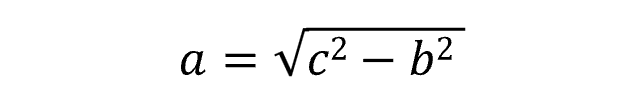
数学や単位の基礎を学ぶには、
「工学知識きその基礎講座」のEラーニングがおすすめです。
文系出身者、数学や単位に自信がない人向けにアニメーションを多用したスライド動画でやさしく解説しています。詳細はこちらから → 工学知識きその基礎講座
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



