���w�̌����ꗗ
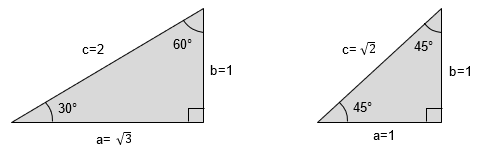
�O�p��
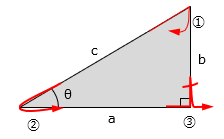 |
�@�@\( \sin\theta = \frac{b}{c}\) (����) |
�t�O�p��
�O�����̒藝�i�s�^�S���X�̒藝�j
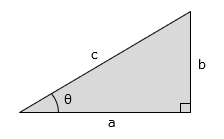 |
\( a^{2}+b^{2}=c^{2} \quad c= \sqrt{a^{2}+b^{2}} \) |
�O�p���̒l
�ǂ��g������ʂȒ��p�O�p�`
�p�x�����ɏ����ȏꍇ
�E\( \sin\theta �� \theta \)
�E\( \cos\theta ��1 \)
�E\( \tan\theta = \frac{\sin\theta}{\cos\theta}��\theta \)
�O�p���̑��݊W
�E\( \sin^{2}\theta+\cos^{2}\theta = 1 \)
�E\( \tan\theta= \frac{\sin\theta}{\cos\theta} \)
���̎O�p��
�E\( \sin(-\theta)=-\sin\theta \)
�E\( \cos(-\theta)=\cos\theta \)
�E\( \tan(-\theta)=-\tan\theta \)
�O�p���̋t��
�E\( \sec\theta= \frac{1}{\cos\theta} \)
�E\( \csc\theta= \frac{1}{\sin\theta} \)
�E\( \cot\theta= \frac{1}{\tan\theta} \)
���ǂݕ��F\(sec\) �i�Z�J���g�j�C\(csc\) ����\(cosec\) �i�R�Z�J���g�j�C\(cot\) �i�R�^���W�F���g�j
������
�E\( \sqrt{0} =0\)
�E\( \sqrt{1} =1\)
�E\( \sqrt{2} =1.41421356�i�����ɐl�����j\)
�E\( \sqrt{3} =1.7320508�i�l���݂ɂ������j\)
�E\( \sqrt{4} =2\)
�E\( \sqrt{5} =2.2360679�i�x�m�R�[�I�E�����j\)
�E\( \sqrt{6} =2.44949�i�ɂ�悭�悭�j\)
�E\( \sqrt{7} =2.64575 �i�ɒ����Ȃ��j\)
�E\( \sqrt{8} =2\sqrt{2}=2.828 \)
�E\( \sqrt{9} =3\)
�w���@��
�E\(a^{m}�~a^{n}=a^{m+n} \)
�E\(a^{m}��a^{n}=a^{m-n} \)
�E\( (a^{m})^{n}=a^{mn} \)
�E\( (ab)^{m}=a^{m}b^{m} \)
�E\( ( \frac{a}{b})^{n}=\frac{a^{n}}{b^{n}} \)
�E\(\frac{1}{a^{m}}=a^{-m} \)
�Ǝ��J�����ꂽMONO�m�́u�X�e�b�v���w�K�v���O�����v���@�l�̗p���сF�V�O�O�Јȏ���
�J�e�S���[���j���[
 �@�B�v�̊�b���w��
�@�B�v�̊�b���w��
 �RDCA�̊�b���w��
�RDCA�̊�b���w��
 �ޗ��͊w�̊�b���w��
�ޗ��͊w�̊�b���w��
 ���̗͊w�̊�b���w��
���̗͊w�̊�b���w��
 ���^�̊�b���w��
���^�̊�b���w��
 �@�B���H�̊�b���w��
�@�B���H�̊�b���w��
 �@�B�v�f�̊�b���w��
�@�B�v�f�̊�b���w��
 �RD�v�����^�[�̊�b���w��
�RD�v�����^�[�̊�b���w��
 �����ޗ��̊�b���w��
�����ޗ��̊�b���w��
 ���}�̊�b���w��
���}�̊�b���w��
 �RDCAD�̉��p���w��
�RDCAD�̉��p���w��
 �M�͊w�̊�b���w��
�M�͊w�̊�b���w��
 �@�B�͊w�̊�b���w��
�@�B�͊w�̊�b���w��
 ���^�̎��H���w��
���^�̎��H���w��
 ���^����T�̃|�C���g
���^����T�̃|�C���g
 CAE��͂̊�b���w��
CAE��͂̊�b���w��
 �v���X�`�b�N�̊�b���w��
�v���X�`�b�N�̊�b���w��
 �d�C�̊�b���w��
�d�C�̊�b���w��
�X�|���T�[�h �����N
���w�̌����ꗗ �֘A�y�[�W
- �@�B�v�Ŏg���P�ʈꗗ
- �͊w�̌����ꗗ
- �P�ʊ��Z�c�[��
- �J���^���d�ʌv�Z�i�����A��S�����A�����A�؍ނȂǁj
- �V�����_���͌v�Z�c�[��
- ���̂���݂Ɖ��͌v�Z�c�[��
- �A�����̂���݂Ɖ��͌v�Z�c�[��
- �f�ʓ��[�����g�v�Z�c�[��
- �����`��̒f�ʂQ�����[�����g�v�Z�c�[��
- �~�̂���݁E���͌v�Z�c�[��
- �����`�̂���݁E���͌v�Z�c�[��
- �����v�Z�c�[��
- �p�x�i���z�j�v�Z�c�[��