
流体力学の基礎が学べるeラーニング販売中!
静止流体から管内や物体周りの流体、そして流体の測定方法に至るまで、流体力学の基礎が理解できる!流速、流量、流線、剥離などの概念をじっくりと掘り下げ、実際の流体の問題解決に役立つ知識が身につく。
質量保存則
気体のように、密度変化を無視できない圧縮性流体の定常流において、下図のような任意の断面(A1やA2)を通過する単位時間あたりに流れる流量(質量流量)は等しくなります。
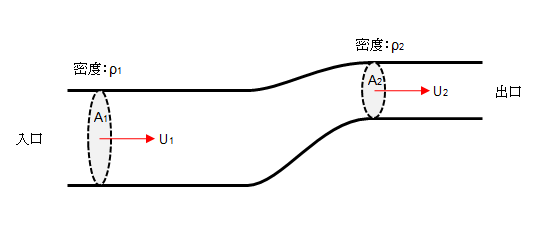
断面Aと断面Bを単位時間あたりに流れる流量を計算してみます。
単位時間をΔtとすると、流れた距離は、速度×時間なので、U×Δt となります。
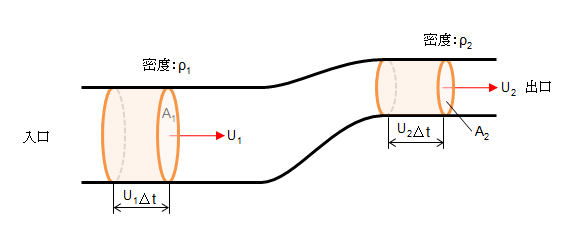
従って、微小時間 Δt 経過後、断面A と 断面Bを通過した質量は、
質量 = ρ×体積 なので
断面Aを通過した質量 = ρ1×(A1×U1ΔT)
断面B を通過した質量 = ρ2×(A2×U2ΔT)
[断面Aを通過した質量] = [断面Bを通過した質量] なので
ρ1×(A1×U1ΔT )= ρ2×(A2×U2ΔT)
ρ2×A2×U2 = ρ2×A2×U2
ρ:密度 A:断面積 U:速度
これを「質量保存則」といいます。
また、密度が一定であれば、ρ1=ρ2 、つまり非圧縮性流体のとき、
A1×U1 = A2×U2 となります。
これを「連続の式」といいます。
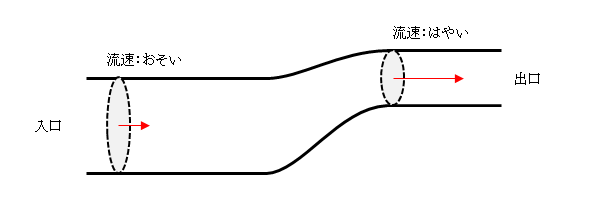
この関係より、単位時間あたりに流れる流体の体積(体積流量)が一定ならば、断面積が大きいほど流体の流速は遅く、断面積が小さければ流速が早いことがわかります。
\ 機械設計者向け「eラーニング」でスキルアップ! /
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
当サイトの記事は、無料会員登録をすることでPDFファイルで読むことができます。また、印刷することも可能です。設計者に必要となる製図、材料力学、機械要素など全部で18種類のテキストを無料でダウンロードしていただけます。
ダウンロードの詳細はこちらからご確認ください。
カテゴリーメニュー
スポンサード リンク



