
若手技術者でも実践的な幾何公差の使い方・考え方が身につく!設計意図からどの幾何公差を入れると良いのかわかるようになる!独学で挫折される方の多い最大実体公差方式も理解し使いこなせる。
幾何公差とは
寸法を制御するものが 「寸法公差」 であるのに対して、 形状を制御するものを 「幾何公差」 といいます。
例えば下図のように 「円の寸法公差」 のみ規定した場合、公差の範囲でゆがんでいたり、中心がずれていたりしても寸法公差の基準は満たしています。「まんまるさ」である真円を守らせるためには幾何公差で「真円度」を規定する必要あります。(中心のずれには「同心度」や「同軸度」を規定)

幾何公差の「幾何」は英語で「ジオメトリー」のことであり、三角形・方形・菱形・多角形・円形などの図形や空間の性質のことです。
幾何公差には 「単独形体」 と 「関連形体」 の大きく2つに分類されます。
単独形体は先ほどの真円度のように その形状自体に指定できるもの です。
関連形体は平行度や直角度のように 相手との関係を指定するもの です。
機械部品は加工機などにより製作されます。製作する過程において様々な誤差が発生します。その誤差の許せる範囲が幾何公差です。業界、製造方法、形状によって異なりますが、一般的に幾何公差を指定する図面は少ないです。なぜなら幾何公差を入れなくてもある程度満足できるレベルのものが仕上がってくるからです。
しかし、精度が要求される部品の場合、幾何公差を指定した方が望ましいです。
幾何公差を指定するには、「加工の知識」 と 「測定の知識」が必要です。なぜなら、どのように加工して、どのように測定するのかを指定するのが幾何公差だからです。
加工や測定の知識といっても、専門的な知識は必要ありません。加工であれば旋盤やフライス盤の加工方法を理解したり、測定器であれば、ハイトゲージや真円度測定器などの測り方を理解しておけば良いです。
幾何公差の種類
幾何公差は、先ほど解説した「単独形状」と「関連形状」の2つに対して、「形状」,「姿勢」,「位置」,「振れ」の大きく4種類に分類されます。
形体 |
幾何公差の種類 |
記号 | 説明 |
※1 | |
|---|---|---|---|---|---|
|
単独形体 |
形状 | 真直度 |  |
直線形体の幾何学的に正しい直線からのひらきの許容値。 | 無 |
| 平面度 |  |
平面形体の幾何学的に正しい平面からのひらきの許容値。 | 無 | ||
| 真円度 |  |
円形形体の幾何学的に正しい円からのひらきの許容値。 | 無 | ||
| 円筒度 |  |
円筒形体の幾何学的に正しい円筒からのひらきの許容値。 | 無 | ||
| 線の輪郭度 |  |
理論的に正確な寸法によって定められた幾何学的輪郭からの線の輪郭のひらきの許容値。 | 無 | ||
| 面の輪郭度 |  |
理論的に正確な寸法によって定められた幾何学的輪郭からの面の輪郭のひらきの許容値。 | 無 | ||
|
関連形体 |
姿勢 | 平行度 |  |
データム直線またはデータム平面に対して平行な幾何学的直線または幾何学的平面からの平行であるべき直線形体または平面形体のひらきの許容値。 | 有 |
| 直角度 |  |
データム直線またはデータム平面に対して直角な幾何学的直線または幾何学的平面からの直角であるべき直線形体または平面形体のひらきの許容値。 | 有 | ||
| 傾斜度 |  |
データム直線またはデータム平面に対して理論的に正確な角度をもつ幾何学的直線または幾何学的平面からの理論的に正確な角度をもつべき直線形体または平面形体のひらきの許容値。 | 有 | ||
| 位置 | 位置度 |  |
データムまたは他の形体に関連して定められた理論的に正確な位置からの点、直線形体、または平面形体のひらきの許容値。 | 有 | |
| 同軸度 |  |
同軸度公差は、データム軸直線と同一直線上にあるべき軸線のデータム軸直線からのひらきの許容値。 | 有 | ||
| 同心度 |  |
同心度公差は、データム円の中心に対する他の円形形体の中心の位置のひらきの許容値。 | 有 | ||
| 対称度 |  |
データム軸直線またはデータム中心平面に関して互いに対称であるべき形体の対称位置からのひらきの許容値。 | 有 | ||
| 振れ | 円周振 |  |
データム軸直線を軸とする回転体をデータム軸直線のまわりに回転したとき、その表面が指定された位置または任意の位置において指定された方向に変位する許容値。 | 有 | |
| 全振れ |  |
データム軸直線を軸とする回転体をデータム軸直線のまわりに回転したとき、その表面が指定された方向に変位する許容値。 | 有 | ||
※1 データムの有無
データムとは、幾何公差を指定した対象を検査する際の基準の面や線のことです。以下で解説。
幾何公差の記入枠
幾何公差を図面に記入する際はルールがあります。長方形の枠内に必要な情報を記入します。
長方形の枠は3つに分かれています。

左の枠内には幾何公差の記号を記入します。
中央の枠内にはばらつきの許容値を記入します。
右の枠内にはデータム記号を記入します。
例えば、真円度を指定する場合、下図のように幾何公差を記入します。
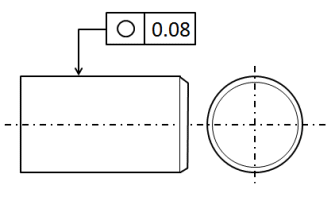
真円度は単独形体なので右側のデータム記号は不要です。
関連形体である 直角度の場合、下図のように幾何公差を記入します。

直角度のように相手との関連公差を指示するときには基準となる面や線が必要となります。
基準となる面や線を データム といい、データム記号をその位置に配置します。
つまり、データムは加工や寸法測定を行う際に、「この面または線を基準に加工・測定しなさい」というものです。
データムの優先順位
下図は位置度を示す幾何公差の記入例です。この例では穴の中心位置をAとBの2箇所から規定しています。2箇所以上の指定がある場合は、優先する順番に左から入れていきます。
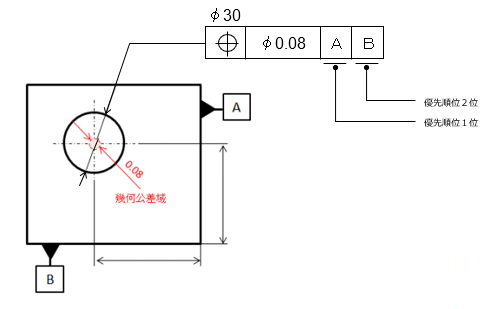
この場合、穴の中心はΦ0.08の幾何公差域に存在しなければなりません。(赤い点線枠内)
尚、データムの優先順位は、一般的に加工機への取り付け順序や部品の組立順序となります。
以上、幾何公差の基本的な内容について解説してきました。幾何公差は、先に説明した寸法公差やはめあい公差よりも使いこなす難易度が高い公差です。なぜなら、幾何公差は部品の形状や位置関係を指定するために全部で15種類の記号の中から選択し、図面で指示する必要があるからです。
また、幾何公差の設定には実務経験が必要な部分が多く、設定を間違えると、部品同士の機能や動作に深刻な影響を与える可能性があります。さらに、幾何公差は部品の形状や位置関係を指定するために使用されるため、正確に計測するための機器や技術が必要であり、そのためには高い技術力や専門的な知識が求められます。
以上のような理由から、幾何公差は使いこなす難易度が高い公差であり、正確に設定するためには多くの努力と経験が必要とされます。
このように習得するための難易度が高い幾何公差を習得するためには、自己学習だけではなく、正しい知識や技術を身につけるための教育が欠かせません。
そのため、弊社ではEラーニングを提供しております。Eラーニングでは、視聴者が自分自身のペースで学ぶことができ、加えて、各種図面を使った演習問題や実際の製品に応用する練習問題を提供しています。これにより、理論だけでなく実践的な技術も身につけることができ、幾何公差の習得に大きく役立ちます。
幾何公差の活用でお困りの方は以下の講座の利用を検討してみてください。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



