
若手技術者でも実践的な幾何公差の使い方・考え方が身につく!設計意図からどの幾何公差を入れると良いのかわかるようになる!独学で挫折される方の多い最大実体公差方式も理解し使いこなせる。
幾何公差の記号一覧
前のページでは、幾何公差の基本について解説しました。こちらのページでは、全部で15種類ある記号について詳しく解説をいたします。幾何公差は、「形状」,「姿勢」,「位置」,「振れ」の4種類に対して全部で15種類の記号が存在します。
真直度
JISでは、「直線形体の幾何学的に正しい直線からの狂いの大きさ」と定義されています。
翻訳すると・・・
真直度は 真っ直ぐさ を指定するものです。平面ではなく直線に適用されます。従って、長尺物などの反りの許容などに利用されます。
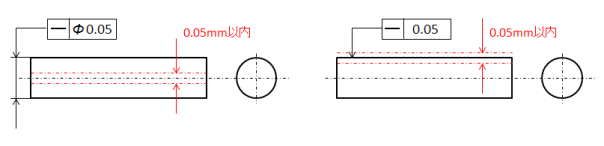
平面度
JISでは、「平面形体の幾何学的に正しい平面からの狂いの大きさ」と定義されています。
翻訳すると・・・
平面といっても厳密には凸凹しています。
平面度は、最も出っ張った部分 と 最もへこんだ部分 が、上下に離れた2つの平面の間に挟まれた一定の距離になければなりません。
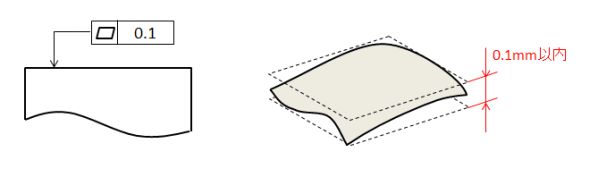
平面度の測定の様子
真円度
JISでは、「円形形体の幾何学的に正しい円からの狂いの大きさ」と定義されています。
翻訳すると・・・
真円度は まんまるさ を指定するものです。

円筒度
JISでは、「円筒形体の幾何学的に正しい円筒からの狂いの大きさ」と定義されています。
翻訳すると・・・
円筒度は まんまる で 真っ直ぐさ を指定するものです。
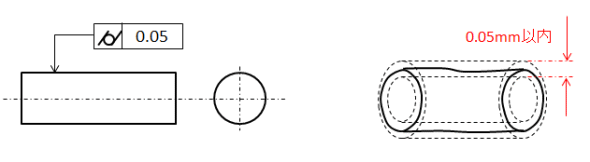
線の輪郭度
JISでは、「理論的に正確な寸法によって定められた幾何学的に正しい輪郭からの線の輪郭の狂いの大きさ」と定義されています。
翻訳すると・・・
線の輪郭度はデザインのある部品の曲面が、デザインした通りに出来ているか指示するものです。
指定の曲面を切断した断面の線が公差域に入っていればOKです。
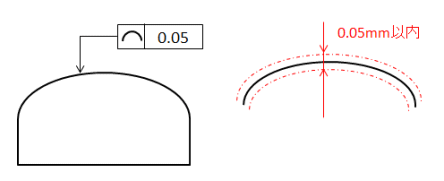
面の輪郭度
JISでは、「理論的に正確な寸法によって定められた幾何学的に正しい輪郭からの面の輪郭の狂いの大きさ」と定義されています。
翻訳すると・・・
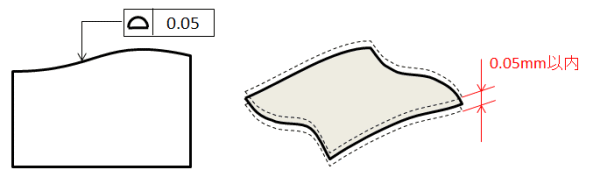
面の輪郭度はデザインのある部品の曲面などが、デザインした通りに出来ているか指示するものです。
面の輪郭度は、線の輪郭度と違って指定曲面全体が対象となります。
平行度
JISでは、「データム直線、データム平面に対して平行な幾何学的直線または幾何学的平面からの平行であるべき直線形体又は平面形体の狂いの大きさ」と定義されています。
翻訳すると・・・
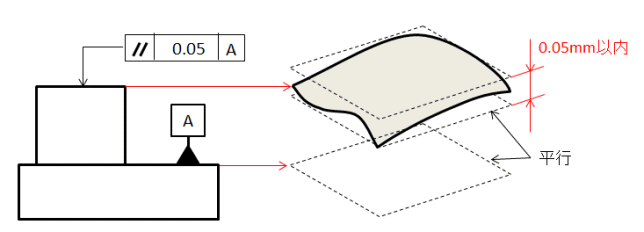
平面度と似ていますが、平行度にはデータム(基準となる平面、直線)が存在します。
(※平面度は形状公差、平行度は姿勢公差。姿勢公差には基準面が必要)
平行度は2つの直線または平面が平行であることを指定します。
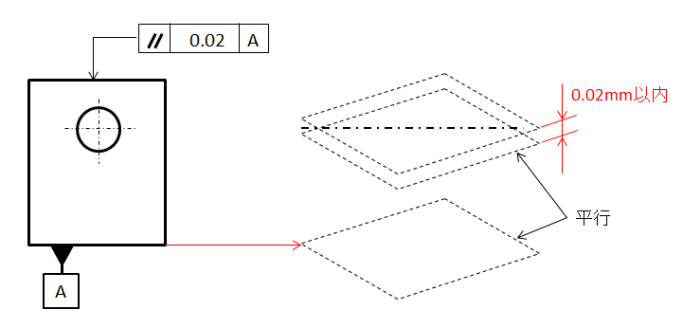
ちなみに、平行度0.1の平面であれば、平面度0.1以下でなければ平行度が満たされません。
直角度
JISでは、「データム直線、データム平面に対して直角な幾何学的直線または幾何学的平面からの直角であるべき直線形体又は平面形体の狂いの大きさ」と定義されています。
翻訳すると・・・
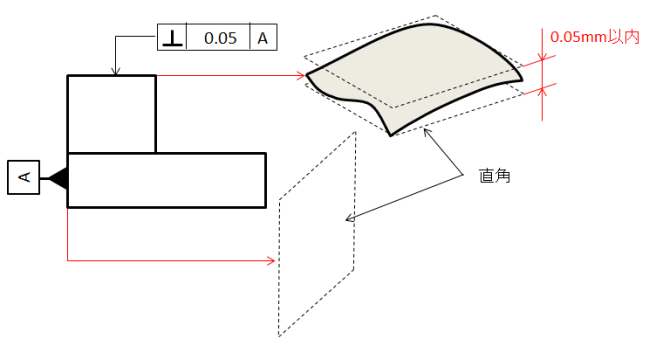
データム(基準となる平面、直線)に対してどのくらい正確に直角であるかを指定します。
直角度で指定する数値は角度ではなく単位は mm です。
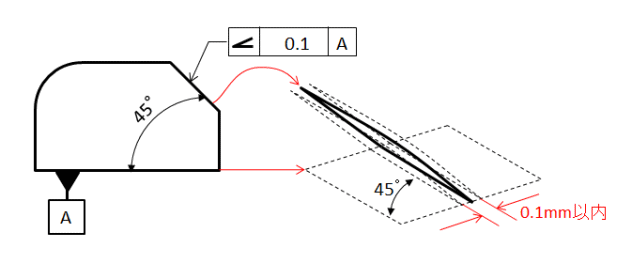
傾斜度
JISでは、「データム直線またはデータム平面に対して理論的に正確な角度をもつ幾何学的直線または幾何学的平面からの理論的に正確な角度を持つべき直線形体及び平面形体の狂いの大きさ」と定義されています。
翻訳すると・・・
傾斜度とは、指定する直線や平面が90°以外であり、データム(基準となる平面、直線)に対して正確に傾斜しているかを指定します。
傾斜度で指定する数値は角度ではなく単位は mm です。
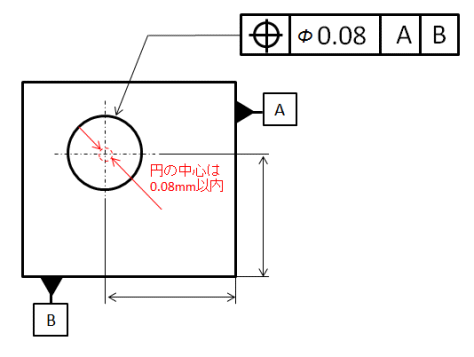
位置度
JISでは、「データム直線または他の形体に関連して定められた理論的に正確な位置からの点、直線形体または平面形体の狂いの大きさ」と定義されています。
翻訳すると・・・
データム(基準となる平面、直線)に対してどのくらい正確な位置にあるかを指定します。
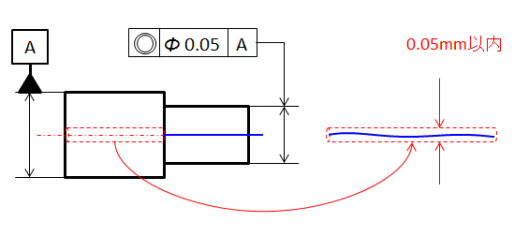
同軸度
JISでは、「データム直線と同一線上にあるべき軸線のデータム軸直線からの狂いの大きさ」と定義されています。
翻訳すると・・・
下図のように、2つの円筒の軸が同軸であること (中心軸がずれていないということ) を指定します。
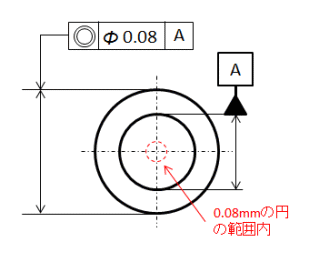
同心度
JISでは、「データム円中心と同一中心上にあるべき点のデータム円中心からの狂いの大きさ」と定義されています。
翻訳すると・・・
下図のように、2つの円筒の軸が同軸であること (中心点がずれていないということ) を指定します。
同軸度との違いは、軸なのか中心点(平面)なのかの違いです。
対称度
JISでは、「データム軸直線又はデータム中心平面に関して互いに対称であるべき形体の対称位置からの狂いの大きさ」と定義されています。
翻訳すると・・・
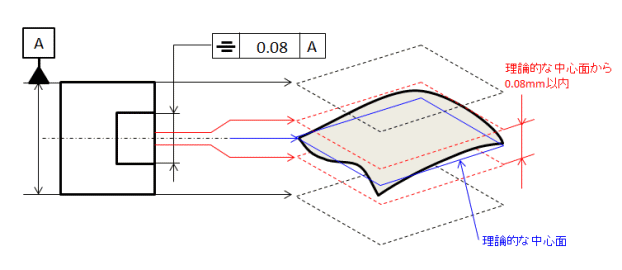
データム(基準となる平面)に対して対称であることを指定します。
図のように上下の2つの面の中心面は±0.04の範囲になければなりません。
円周振れ
JISでは、「データム軸直線を軸とする回転面を持つべき対象物又はデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した位置又は任意の位置で指定した方向に変位する大きさ」と定義されています。
翻訳すると・・・
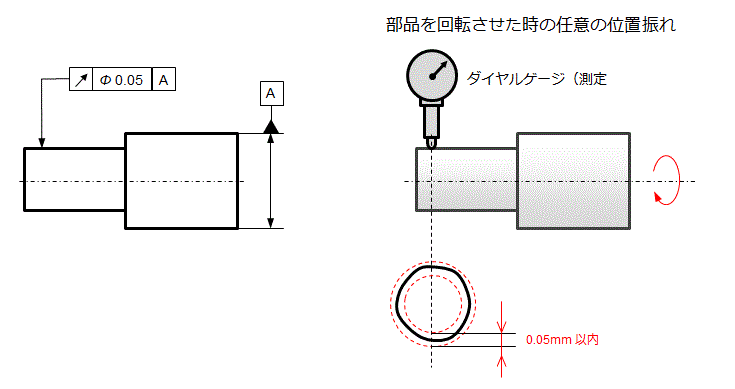
部品を回転させたときの任意の円周の一部の振れを指定します。
円周振れは下図のように部品を回転させたときのダイヤルゲージの振れの範囲になければなりません。
全振れ
JISでは、「データム軸直線を軸とする回転面をもつべき対象物又はデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転した時、その表面が指定した位置又は任意の位置で指定した方向に変位する大きさ」と定義されています。
翻訳すると・・・
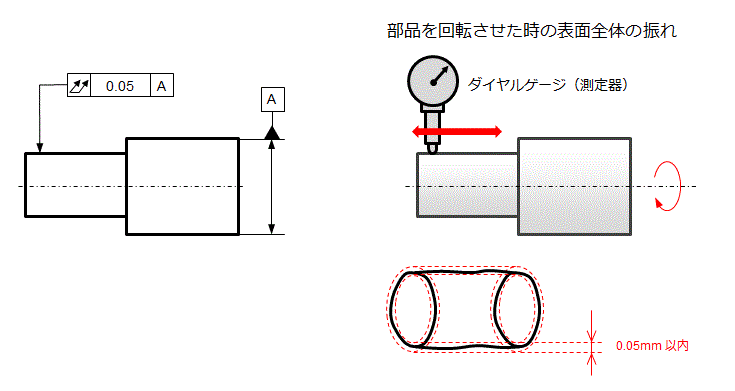
部品を回転させたときの表面全体の振れを指定します。
全振れは下図のように円筒面全体のダイヤルゲージの振れが規定の範囲になければなりません。
以上のように、幾何公差には多くの記号があり、正確に覚えて使いこなすには多くの努力と時間が必要です。弊社ではこのように難易度が高い幾何公差を効率的に学べるEラーニングを提供しています。
Eラーニングを使えば、自分のペースで学ぶことができ、繰り返し学習することで記憶に定着させることができます。
弊社が提供するEラーニングでは、3Dモデルを使ったビジュアル的な教材が多く採用されており、幾何公差の記号や特性を理解しやすくなっています。
幾何公差は設計者だけでなく加工者や測定者にとっても必要なスキルであり、図面を必要とする幅広い技術者が学ぶことができます。
また、Eラーニングは時間や場所を選ばずに学習できるため、仕事の合間や自宅など、自分に合った時間や場所で学習することができます。さらに、学習記録を残すことができるため、自分がどこまで学習したか、どこがまだ理解できていないかなど、自分の進捗状況を確認することができます。
以上のように、Eラーニングを活用すれば、15種類の幾何公差の記号を効率的に学ぶことができます。ぜひ、Eラーニングを活用して、幾何公差のマスターを目指してみてください。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



