知識ゼロの初心者でも図面が描けるようになるの?立体から平面へ、平面から立体へ図形をイメージする方法から「はめあい」や「表面粗さ」などの各種記号の使い方を演習を交えて徹底的に学びます!
ねじの表し方
「ねじ」 は使用する目的に応じてとても多くの種類が存在します。
その中でも最もスタンダードであるボルトの描きかたについて説明します。
雄ねじの表記方法
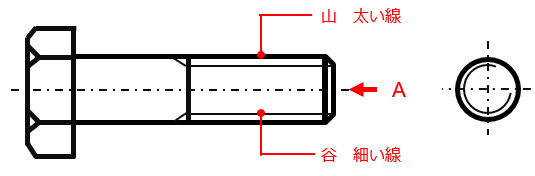
ボルト(雄ねじ) には、山と谷 が存在します。
ボルトを図のAの方向から見たとき、谷の形状は山の形状に隠れて見えません。
従って、ボルト(雄ねじ)部を図面に表記する場合、
山 の部分は 太い実線
谷 の部分は 細い実線
で描きます。
雌ねじの表記方法
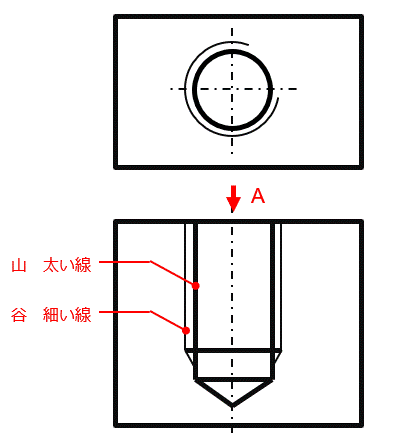
次に雌ねじですが、雌ねじを図の方向から見たとき、雄ねじ同様に谷の形状は、山の形状に隠れて見えません。
従って、雌ねじ部を図面に表記する場合、
山 の部分は 太い実線
谷 の部分は 細い実線
と雄ねじと同様になります。
但し、雄ねじと雌ねじでは山谷が入れ替わるため、雌ねじでは外側が細線、内側が太線となりますので注意が必要です。
不完全なねじ部の表記方法
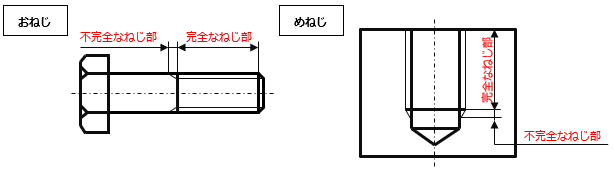
ボルトのねじが切られた最後の部分は不完全なねじ部となっています。
不完全な ねじ部の谷底は図のように斜めの線で示します。
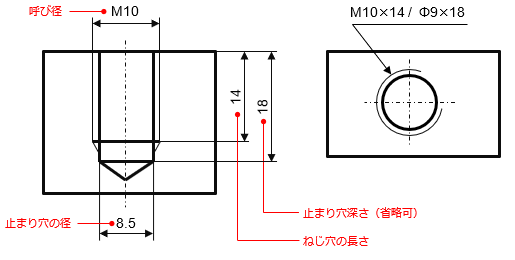
ねじの種類及び寸法記入方法
ねじには非常に多くの種類が存在します。ねじの種類及び寸法は規格に規定される呼び方で図示します。
例えば良く利用されるメートルねじの場合、図のように引出線を用いて、ねじの種類(M10)を記入します。
(ねじの種類には様々です。略号(M、Gなど)を用いて表記します。)
ねじ長さ寸法は、不完全ねじ部を除いた長さを記入します。
(左下図では14の寸法がねじ長さの寸法です。)
また、下穴となる止まり穴深さを指定しない場合、ねじ長さの1.25倍程度に描きます。
(左下図では18の寸法が止まり穴深さの寸法です。)
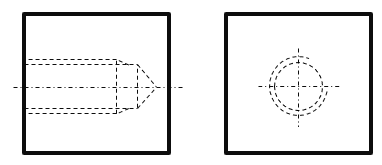
ねじの隠れ線
隠れたねじを示す場合、山と谷を表す線は細い破線で表します。
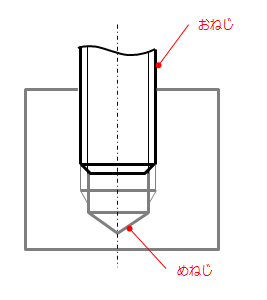
雌ねじと雄ねじを組み合わせた際の製図方法
最後に雌ねじと雄ねじを組み合わせた際の製図方法を説明します。
雄ねじは外側が太線、雌ねじは外側が細い線です。重なる線はどちらを優先させるかというと、下図に示すように雄ねじを優先して作図します。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



