知識ゼロの初心者でも図面が描けるようになるの?立体から平面へ、平面から立体へ図形をイメージする方法から「はめあい」や「表面粗さ」などの各種記号の使い方を演習を交えて徹底的に学びます!
寸法補助記号の一覧表
寸法値の前に「補助記号」を付けることで、寸法値に対して意味を持たせることが可能となります。
(例) 半径10mmの円 = R10 Rは半径という意味
R10と図面に書けば、JISの図面ルールを知っている人は、瞬時に半径が10mmであることが理解できます。
「寸法補助記号」はその寸法値が何を表しているのか明確にでき、読み手の理解を助ける役割を持ちます。
R以外に様々な寸法補助記号がJISで規定されています。
以下は、JIS Z 8310で規定されている寸法補助記号の一覧です。
記号 |
記号の意味 |
呼び方 |
|---|---|---|
R |
半径 |
あーる |
Φ |
直径 |
まる・ふぁい |
□ |
正方形 |
かく |
SΦ |
球の直径 |
えすまる・えすふぁい |
SR |
球の半径 |
えすあーる |
t |
厚み |
てぃー |
C |
面取り |
しー |
これらの「寸法補助記号」の具体的な使い方は「寸法の表し方」で解説します。
寸法補助記号を使う上での注意点
寸法補助記号を使う際はいくつかの注意点があります。
以下は、最も良く利用される円の寸法補助記号Φの使い方です。
JISでは下図に示す通り、円の形が分かる形状に寸法を入れる場合は寸法補助記号の「Φ」を省略することになっています。
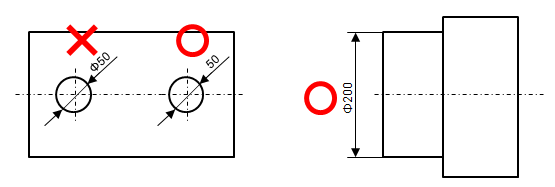
しかし、実際の設計図面で円の形が分かる形状にも「Φ」をつけているケースは良くあります。
JIS規定と異なるから間違っている図面ということではありません。
図面を作成する上で重要なことは、読み手に対して認識の違いを与えないことです。
穴形状の寸法に「Φ」が入ることで図面の読み違いが発生することはありえません。
従って、JISの規定はあくまでも基本的なルールであって、絶対ではないということを理解しておく必要があります。
また、図面のルールは会社独自に作られるケースも存在します。つまり読み手に対して認識の間違いを防ぐことが重要であるということです。
独自開発されたMONO塾の「ステップ式学習プログラム」<法人採用実績:700社以上>
カテゴリーメニュー
スポンサード リンク



